Capitolo 27 ) Correlazione

Date due serie di dati, x_n e y_n , si può analizzare la loro reciproca dipendenza (o, al contrario, la loro indipendenza) con metodi derivati dall’analisi statistica. Quale esempio si considerino i dati di peso corporeo e di altezza relativi a ciascuno degli N individui di una popolazione.

Ipotizzando una relazione lineare fra i dati delle due serie, si possono così calcolare i parametri che definiscono una retta rappresentante idealmente l’andamento di una delle variabili rispetto all’altra.

Questo procedimento è noto come analisi di regressione lineare.

Ovviamente, anche quando questa relazione esiste, i dati possono non essere allineati su una retta (per effetto di una certa casuale distribuzione dei valori), quindi si tratta di stabilire un criterio che minimizzi gli scostamenti dei dati reali dalla retta ideale.

Il criterio maggiormente seguito è quello del minimo scostamento quadratico medio, cioè di rendere minima la somma degli scostamenti fra ogni punto (definito dai valori di x e y corrispondenti allo stesso indice n) e la retta stessa.

Risulta intuitivo che esiste una reciprocità di dipendenza a secondo che si consideri come variabile indipendente la x oppure la y : nel primo caso è

y = a·x + b, con a e b i parametri cercati, dove a è la pendenza della retta e b l’intercetta per x=0.

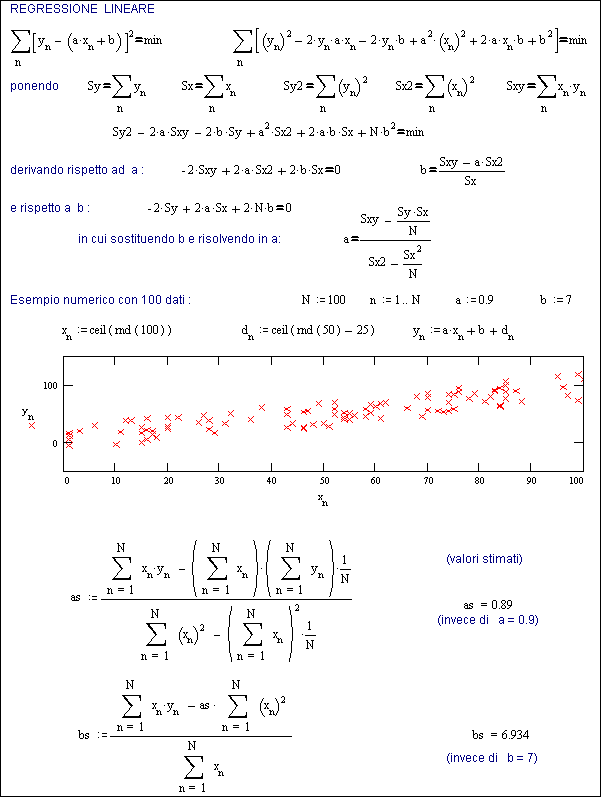
La Fig.27.1a mostra i passaggi algebrici che consentono di ricavare tali parametri. Per minimizzare la sommatoria dei quadrati delle differenze, si sviluppa questa espressione e si uguagliano a zero la derivate parziali rispetto ad a ed a b.

Un esempio numerico, con N = 100 dati, permette di verificare il metodo.

La serie di dati y_n, è ricavata con parametri noti a priori, ma vengono introdotti disturbi (d_n) fino al 25%, come si può vedere dal grafico.

Malgrado ciò, i valori stimati (as e bs) non si discostano significativamente da quelli utilizzati per stabilire i valori di y .

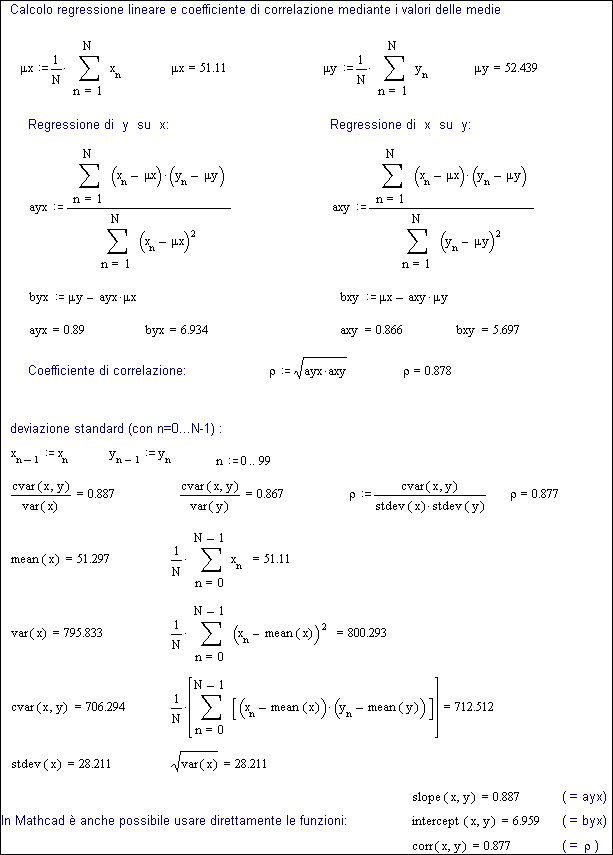
La Fig.27.1b mostra invece gli stessi calcoli utilizzando le funzioni statistiche, in particolare la media aritmetica (m).

Per quanto già accennato, in generale vi sarà una differenza se come variabile indipendente si considera la x o la y, cioè se si cerca la regressione di y rispetto a x o viceversa di x rispetto a y (in altre parole i coefficienti ayx e byx, oppure axy e bxy).

Quindi si potranno avere due rette y = ayx · x + byx e x = axy · y + bxy

distinte.

Il legame fra x e y sarà tanto più probabile quanto più coincidenti saranno queste due rette, e il parametro che esprime questa dipendenza è

detto coefficiente di correlazione (r) , ed è dato dalla radice quadrata del prodotto delle due pendenze.

Fig.27.1a - Metodo di regressione lineare fra due serie di dati.

Fig.27.1b - Calcolo di regressione e correlazione con funzioni statistiche Mathcadâ.

Poichè nel caso di massima corrispondenza le due pendenze dovrebbero risultare inverse (una relativa all’asse x e l’altra relativa all’asse y), il massimo di r è uguale ad 1

Nel caso di indipendenza delle due serie di dati, le relative rette di regressione risulterebbero perpendicolari fra loro, quindi r tenderebbe a zero.

Il calcolo con Mathcadâ è facilitato dall’uso di speciali funzioni statistiche, che corrispondono a importanti concetti e che quindi meritano di essere approfonditi.

Oltre alla ben nota media aritmetica ( mx = mean(x), in Mathcadâ) è importante il concetto di varianza ( var(x) ), che esprime la distribuzione dei dati attorno alla media ed è definita appunto dalla sommatoria dei quadrati delle differenze di ciascun dato rispetto alla media.

La radice quadrata della varianza esprime la ben nota deviazione standard ( stdev(x) ), valore che ha un particolare significato se la distribuzione dei dati è di tipo ‘gaussiano’ (cioè con un andamento a forma di campana attorno al valor medio), come normalmente assunto in fenomeni casuali.

Quando si hanno due serie di dati, come considerato nelle Fig.27.1a e b, è anche importane il concetto di covarianza ( cvar(x,y) ), che esprime la sommatoria dei prodotti delle singole differenze dei dati rispetto alle relative medie (vedi Fig.27.1b, che riporta le singole funzioni ed il loro sviluppo secondo le definizioni).

Va infine segnalato che se il problema è limitato alla ricerca delle retta di regressione e alla valutazione della correlazione, il Mathcadâ dispone delle funzioni dirette, quindi è possibile utilizzare semplicenente slope(x,y), intercept(x,y) e corr(x,y) per ricavare i rispettivi valori.

Se la relazione che lega le due serie non fosse di tipo lineare, il Mathcadâ potrebbe ancora essere utilizzato per valutare regressioni quadratiche (paraboliche) o cubiche, e persino funzioni generali predefinite.

Quello che però interessa più strettamente l’elaborazione dei segnali è il caso in cui le coppie di valori x_n e y_n sono valori rilevati al tempo t_n (cioè con t_n = n·Dt ), caso in cui la correlazione assume significati particolari.

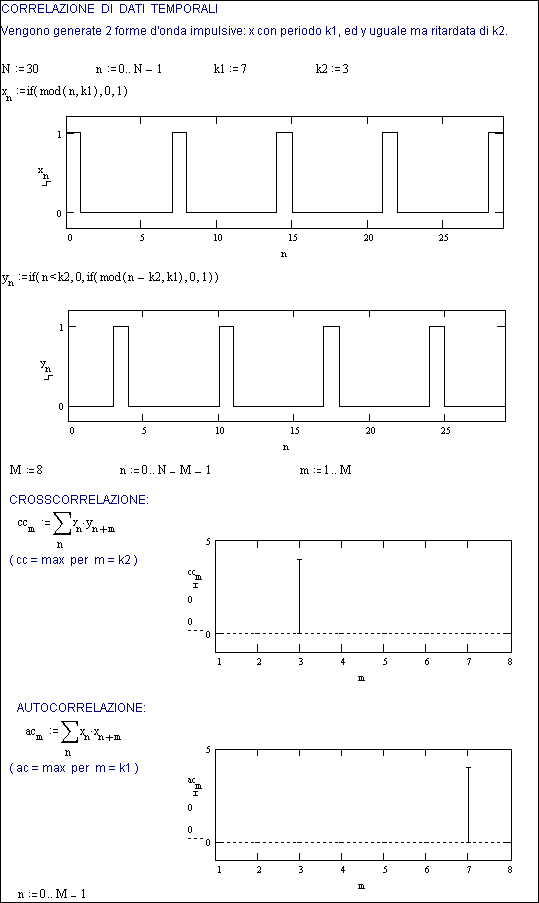
La Fig.27.2 mostra la generazione di due segnali impulsivi di periodo k1·Dt , con un ritardo di k2·Dt del secondo (y) rispetto al primo (x).

Se ora si fa la sommatoria dei prodotti dei due segnali per ciascun intervallo di campionamento ed estesa ad un periodo M·Dt , si nota un massimo in corrispondenza di k2. Ciò significa che mediante la correlazione è possibile rilevare il ritardo fra due forme d’onda simili.

Fig.27.2a - Principio della correlazione fra serie di dati temporali

Ovviamente il calcolo delle sommatorie deve essere esteso ad un periodo che comprenda il ritardo, ed il fatto che si considerino i prodotti dei valori di entrambi i segnali (prodotti ‘incrociati’) dà il nome di crosscorrelazione a tale calcolo.

Si può osservare anche che se al posto del secondo segnale si utilizzano i valori dello stesso, si ottiene un’ autocorrelazione. Il risultato è che si ottiene il massimo in corrispondenza del periodo del segnale stesso, cioè k1.

Queste semplici osservazioni sono la base di importantissime applicazioni nell’elaborazione dei segnali: basti pensare agli ecoscandagli, dove segnali sonori permettono la misura dei fondali marini, ma anche ai radar, dove gli echi di segnali elettromagnetici permettono la localizzazione di ostacoli, fino ai più recenti misuratori di velocità basti sui laser, ed ai localizzatori satellitari (GPS).

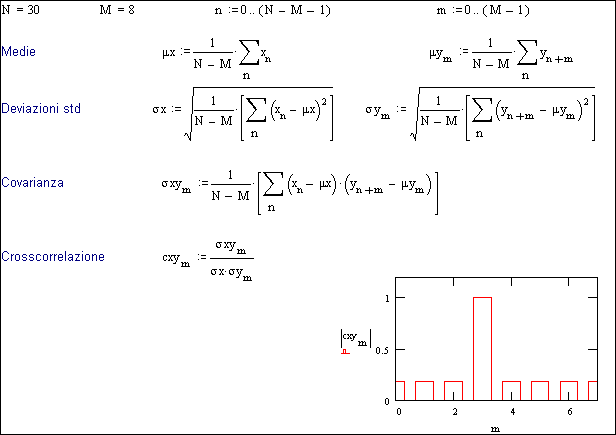
Fig.27.2b - Procedura alternativa di calcolo della crosscorrelazione.

La Fig.27.2b riporta lo sviluppo dei calcoli necessari per trovare l’andamento della crosscorrelazione, utilizzando le definizioni illustrate nella Fig.27.1b.

Si deve però osservare che il numero n di dati considerato è N-M e che la procedura è ripetuta per M volte, con l’indice m=0..M-1.

Quindi i primi N-M dati di x vengono moltiplicati per lo stesso numero di dati di y, iniziando però la serie dall’ m-esimo dato.

Nel caso esaminato, data l’uguaglianza di y rispetto ad x (salvo il ritardo) risulta che la crosscorrelazione è massima (cxy = 1) in corrispondenza di m = 3, cioè del ritardo k2, come indicato dal grafico.

Se al posto di y si mettesse x , si avrebbe un’autocorrelazione e quindi risulterebbe cxx = 1 in corrispondenza di m = 7 , cioè del periodo k1, come del resto già visto in linea di principio nella Fig.27.1b.

Osservando in Fig.27.2b il calcolo della covarianza si nota che la sua struttura è simile a quella della convoluzione, quindi è spontaneo pensare che questo procedimento (lunghe sommatorie di prodotti) possa essere semplificato passando nel dominio delle frequenze, cioè utilizzando le trasformate di Fourier.

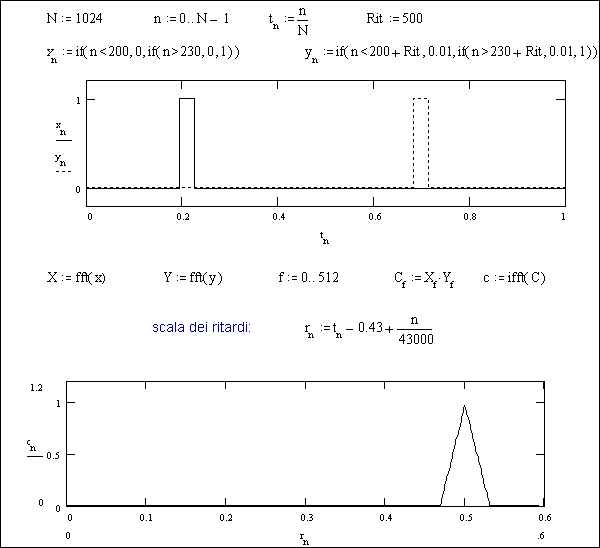
Fig.27.3 - Applicazione delle trasformate di Fourier al calcolo di correlazione.

La Fig.27.3 mostra questo metodo, in cui vengono moltiplicati fra loro solo i singoli coefficienti delle varie frequenze ( X_f e Y_f ) per poi antitrasformare il risultato.

La correlazione c è poi rappresentata in un grafico in funzione del ritardo rilevato fra le due serie: la scala di questo (r_n) è funzione lineare del tempo, ed in questo caso è stata ricavata empiricamente.

Per approfondire questo metodo, che ha importanti applicazioni pratiche, è però opportuno introdurre i concetti di potenza di un segnale e degli spettri di potenza.