Capitolo
26 )
Sistemi con ritardo
Oltre alle costanti di
tempo che caratterizzano i sistemi da controllare, può essere riscontrato in
alcuni di questi un ritardo (delay) sul segnale in
uscita, rispetto al segnale in ingresso, ritardo che complica non poco la
regolazione del sistema.
Spesso tale ritardo è
dovuto semplicemente al rilevatore del segnale in uscita, ad esempio se questo
è situato ad una certa distanza dalla posizione in cui forma il segnale stesso.
Per chiarire una situazione di questo tipo, è opportuno
ricorrere alla comune esperienza della doccia: se si tenta di regolare
bruscamente la temperatura dell’acqua si rischia di oscillare fra momenti di
acqua caldissima e momenti di acqua
fredda senza raggiungere la temperatura desiderata.
Ciò è dovuto al
ritardo di percezione causato dalla distanza che l’acqua deve percorrere fra i
rubinetti di miscelazione (regolatore) ed il corpo (sensore), quindi dal
tempo che impiega l’acqua a percorrere tale distanza.
Nel caso di regolatori
automatici classici (analogici), la presenza di un ritardo puro che non sia trascurabile nei confronti delle
costanti di tempo, costringe in generale ad un abbassamento delle prestazioni,
rendendo soprattutto lento l’anello chiuso di regolazione.
Al contrario, i
regolatori digitali hanno intrinsecamente la possibilità (almeno in linea
teorica) di annullare l’effetto del ritardo, sia questo costante o variabile.
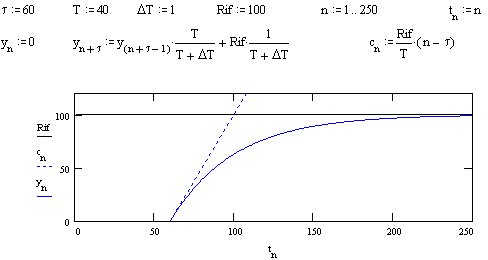
Fig. 26.1 - Risposta a un gradino (Rif = 100) di un sistema con costante di tempo (T = 40)
e ritardo (t = 60).
La Fig. 26.1 mostra in
dettaglio l’effetto del ritardo sulla risposta del sistema, ed è facile
immaginare che se un tale sistema si trova all’interno di un anello chiuso di
regolazione contenente un integratore, quest’ultimo continua ad integrare il
massimo dell’errore per tutto il tempo di ritardo, con conseguente saturazione.
Solo quindi un tempo
di integrazione che sia molto più lungo del ritardo, consente di stabilizzare
l’anello ma, come si è detto, con conseguente rallentamento della risposta
complessiva.
Per evitare tale
inconveniente, si dovrebbe disporre di una retroazione ‘depurata’ dal ritardo, costruendo un blocco
che abbia le medesime caratteristiche del sistema (cioè gli stessi guadagni e
le stesse costanti di tempo) ma senza il ritardo.
Matematicamente, il
ritardo t
può essere espresso con la sua trasformata di Laplace e-ts (vedi
tabella al capitolo 7) per renderla
compatibile con le espressioni delle funzioni di trasferimento, ed in tal caso
la funzione di un blocco rappresentante il processo da controllare risulta e-ts·Gp(s), dove Gp(s)
è appunto la pura funzione di trasferimento.
La Fig. 26.2a
mostra una possibile soluzione del problema posto, nota come predittore
di Smith.
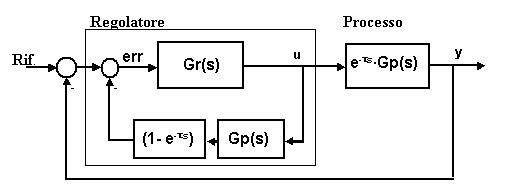
Fig. 26.2a - Configurazione di regolazione con predittore
di Smith.
Una semplice analisi
del comportamento di tale configurazione 1)
evidenzia infatti che il regolatore non
‘vede’ più il ritardo, risultando equivalente alla configurazione
della Fig. 26.2b.
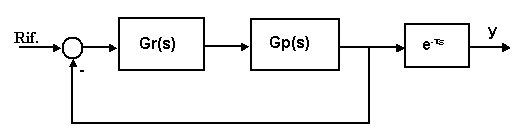
Fig. 26.2b - Configurazione equivalente al predittore di
Smith
Il problema è così
teoricamente risolto, salvo l’osservazione che
Gp(s) deve essere esattamente
identificato e che deve ritenersi assolutamente costante, ma la realizzazione pratica del predittore di Smith con tecniche
analogiche rimane difficoltosa.
![]()
1) Dalle relazioni err = Rif - y - u·(1-e-ts)·Gp u = err·Gr = y / (e-ts·Gp)
eliminando err ed u, si può ricavare y/Rif = e-ts·(Gr·Gp/ (1+Gr·Gp)) , cioè la funzione di trasferimento globale che corrisponde alla Fig. 26.2b.
Il ricorso a tecniche
digitali semplifica la soluzione, osservando che in questo campo il
ritardo t è esprimibile semplicemente come z - n(t), dove
n(t) = t / DT 26.2) .
Ciò significa che il ritardo può essere espresso
in un numero n(t) di
campionamenti DT equivalente
a t.
La funzione di
trasferimento in forma digitale (funzione in
z) del processo è quindi semplicemente la S(z), come visto a
pag. 22-1, moltiplicata per il
ritardo z-n(t).
L’errore all’ingresso del regolatore con predittore
di Smith è allora
err = Rif - y - u·(1- z-n(t))·S(z) mentre l’uscita è u =
err·R(z)
Supponendo per
semplicità che il processo abbia una sola costante di tempo ed il regolatore
sia di tipo PI, si ha
S(z) = a0s / (1- b1s·z-1) e R(z) = (a0r + a1r· z-1) / (1-
b1r·z-1)
Utilizzando i
coefficienti ottimizzati per avere una risposta complessiva Td
(fig. 22.2 ) è possibile simulare il comportamento dell’intero sistema
calcolando per ogni istante n·DT
i valori di err, u e y.
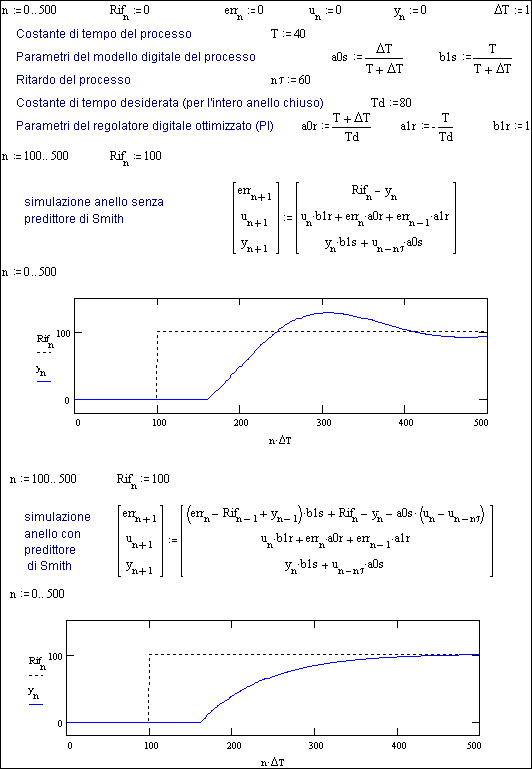
La Fig. 26.3 simula questo comportamento sia
con semplice regolatore PI, sia con l’aggiunta del predittore di Smith.
Si sono mantenuti per
il processo gli stessi valori della Fig.26.1, e si è ipotizzata una risposta
complessiva desiderata Td = 80 (ms).
Malgrado questa scelta
di risposta abbastanza lenta (il doppio
di T) si dimostra che senza predittore si ha una sovraelongazione del 25%,
quindi inaccettabile.
Una scelta di risposta
più veloce porterebbe ad un andamento decisamente oscillatorio e solo
l’inserimento del predittore consente
di ottenere una risposta ottimizzata.
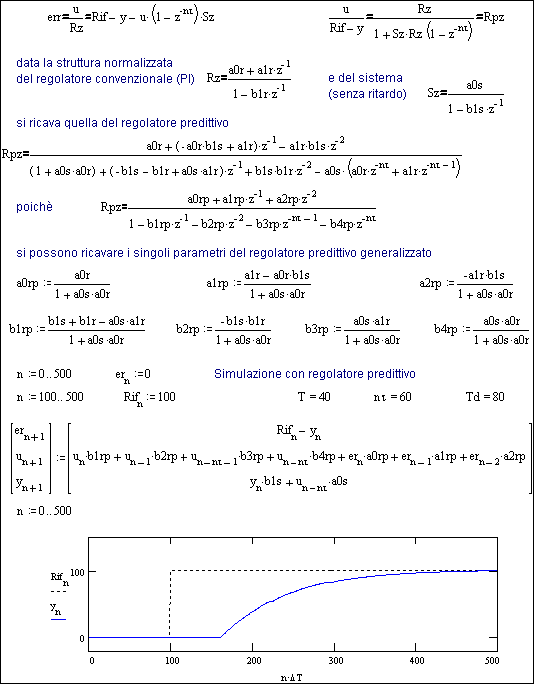
La Fig.26.4 mostra una
possibile implementazione del regolatore predittivo con il calcolo algebrico
dei parametri di una struttura generalizzata (3 al numeratore e 4 al denominatore), dalla quale potrebbero
essere ricavati i coefficienti di strutture normalizzate (occorrerebbero 2
blocchi biquadratici, vedi cap.18).
Si evidenzia che il
valore dei coefficienti può essere molto critico, per cui deve essere valutato
l’effetto degli inevitabili arrotondamenti.
|
|
Fig. 26.3 - Simulazioni del comportamento di un processo con
ritardo, regolato senza e con predittore di Smith.
Si sottolinea inoltre
che, come già citato, simili soluzioni richiedono la perfetta conoscenza dei
parametri del processo (nonchè la loro costanza nel tempo), il che ne potrebbe
rende impraticabile l’impiego.
Per questi casi, si
consiglia un approccio sempre digitale, meno teorico, ma senz’altro più
‘affidabile’.
Uno dei metodi più
banali per diminuire gli inconvenienti del ritardo è una regolazione
campionata, che agisca cioè solo in determinati istanti, rimanendo poi in
attesa, prima di esaminare l’effetto conseguito.
In altre parole, la
regolazione viene periodicamente ‘congelata’, per permettere che il sistema si
stabilizzi prima di effettuare un’ulteriore correzione.
|
|
Fig. 26.4 - Calcolo
parametri del regolatore predittivo normalizzato e simulazione del
sistema risultante (anello chiuso).