G. Schgör (Lugl. 2004, agg. Nov. 2005)

La simulazione con calcolatore nella didattica degli amplificatori operazionali

Sommario

Vengono illustrati programmi per calcolatore che illustrano i principi e le più importanti configurazioni applicative degli amplificatori operazionali.

Iniziando dai circuiti di amplificazione a transistor, viene infatti prima simulata la struttura dell’operazionale per poi passare alle configurazioni lineari e non-lineari di questo componente fondamentale per l’elettronica analogica.

Una serie di programmi è poi dedicata alle risposte in frequenza degli amplificatori retroazionati, per una più immediata comprensione degli effetti che la retroazione produce sul comportamento dell’amplificatore stesso.

Un’altra serie ne mostra le principali applicazioni pratiche, dai filtri al calcolo analogico e alla regolazione automatica.

La rassegna di questi programmi si conclude con la simulazione di anelli di regolazione automatica di tipo proporzionale(P), proporzionale-integrale (PI) e proporzionale-integrale-derivativa (PID), con possibilità di associare le risposte in frequenza (diagrammi di Bode) con le risposte nel tempo dell’anello stesso, permettendo così progettazione e verifica delle prestazioni del regolatore.

Ad ogni modo, i programmi qui citati sono scaricabili gratuitamente, clickando sul singolo riferimento.

I programmi sono degli eseguibili da VisualBasic (.exe) e non richiedono particolari requisiti per la loro esecuzione in ambiente Windows (salvo la presenza dell’interprete VBRUN300.dll, normalmente già esistente nel software di base del computer).

Premesse

Gli amplificatori operazionali, apparsi alla fine degli anni sessanta, hanno rivoluzionato l’elettronica analogica, introducendo possibilità di calcolo che permisero di risolvere brillantemente gran parte dei problemi posti dall’evoluzione dell’automazione industriale e delle comunicazioni.

Giustamente quindi questi elementi vengono illustrati nei libri di testo dei corsi di elettronica delle nostre scuole, anche se gli indirizzi attuali dell’elettronica sono sempre più orientati a soluzioni ‘digitali’ anziché analogiche.

Questa considerazione però dovrebbe portare ad un diverso modo di insegnare l’elettronica, non insistendo per esempio in inutili particolari e non facendo sfoggio di altrettanto inutile trattazione ‘matematica’ , spesso fine a sé stessa e che penso non lasci traccia negli studenti alla fine degli studi.

La proposta alternativa è una più immediata forma di comprensione, oggi permessa dall’uso del calcolatore, basata sulla ‘simulazione’ del comportamento dell’elemento inserito in una particolare configurazione circuitale, una sorta di ‘laboratorio virtuale’ in cui con estrema facilità si comprendono gli effetti delle variazioni introdotte (cambi di parametri o di configurazione).

Naturalmente l’utilizzo didattico di tali programmi richiede la guida da parte di un Docente, che ne illustri i principi e che indichi agli studenti i più opportuni obiettivi di ricerca, a meno che non si sviluppino corsi in rete per permettere anche un uso autodidattico dei programmi stessi.

1) Dal transistor all’amplificatore operazionale

Il primo programma considerato (trans.exe) richiama definizioni di transistor ed il concetto di amplificazione di corrente(b), illustrando poi la classica configurazione ad emettitore comune, come amplificatore di tensione.

Di questa configurazione viene dato un elementare circuito equivalente, che permette di capire i concetti di polarizzazione e dell’amplificazione di un segnale, con possibilità appunto di ‘sperimentarne’ il funzionamento.

Così vengono anche presentate le configurazioni ad ‘emitter follower’ e a ’generatore di corrente’, propedeutiche per l’introduzione dell’amplificatore differenziale, cioè della base su cui è stato sviluppato l’amplificatore operazionale.

Come si potrà notare dall’uso di tali programmi, la didattica è ridotta all’essenziale, ma l’osservazione del funzionamento di questi circuiti permette una facile assimilazione dei concetti fondamentali, quindi un apprendimento più concreto e duraturo.

2) Impieghi dell’amplificatore operazionale

Il secondo programa (opamp.exe) permette di chiarire il ruolo del ‘guadagno’ dell’amplificatore per raggiungere la pratica parità del segnale d’uscita rispetto a quello d’ingresso (a parte il segno).

Questo fa capire in modo elementare la funzione di ‘moltiplicatore per una costante’ intrinseca nella configurazione di base dell’amplificatore reazionato e dato dal rapporto fra resistenza d’ingresso e quella di retroazione.

Così risulta anche evidente la possibilità di ‘somma’ di due o più segnali.

Concettualmente più complessa è la configurazione per ‘integrare’ un segnale, ma qui le difficoltà possono derivare da insufficienti basi matematiche o di elettrotecnica (comportamento circuitale del condensatore), non certo dalla comprensione del circuito.

L’applicazione si riferisce solo al cambiamento della costante d’integrazione (RC), ma è sufficiente per far capire l’effetto di questa sull’andamento dell’uscita con segnale d’ingresso costante.

L’ultima voce di questo programma riporta un’immediata applicazione degli amplificatori operazionali nello studio del comportamento dinamico di una configurazione meccanica (un peso appeso ad una molla) sottoposta ad una forza.

Pur essendo anacronistico l’uso di un ‘simulatore analogico’, questo è un buon esempio di impiego degli amplificatori operazionali nel calcolo, con la tipica soluzione di un’equazione differenziale del secondo ordine, permettendo almeno di capire le possibilità di applicazione, prima dell’avvento dei calcolatori elettronici.

Ritorneremo comunque sull’argomento, con una più recente serie di programmi, che illustra anche il caso di soluzione simultanea di equazioni lineari.

3) Impieghi non-lineari degli amplificatori operazionali

Un altro importantissimo campo di applicazioni riguarda il trattamento non-lineare dei segnali ed un programma apposito (Nolin.exe) ne illustra i principali esempi.

Il primo esempio riguarda la simulazione del comportamento del diodo ideale, che permette un facile approccio al concetto di non-linearità fra segnali di ingresso e di uscita (compresa la saturazione, quasi mai evidenziata nei libri di testo).

Certamente più notevole è la generazione di funzioni speciali, quali quella quadratica del secondo circuito: la visualizzazione del cambiamento di pendenza, cioè del rapporto fra uscita ed ingresso, è evidenziato dalla simulazione con l’indicazione del punto di lavoro che si sposta lungo le rette che approssimano la funzione.

Ancora più spettacolare è la simulazione del ‘rilevatore di soglia’ di un segnale, che permette di cogliere immediatamente i concetti non banali di ‘valore di soglia’ e di ‘zona morta’ (cioè i limiti di intervento del bistabile), con la possibilità di variare tutti i parametri che ne determinano il funzionamento.

Dello stesso livello di importanza è il circuito astabile, cioè il classico oscillatore ad onda quadra.

Anche in questo caso, dopo la presentazione del principio di funzionamento, è simulata la generazione non solo della frequanza variabile, ma viene considerata anche la possibilità di variare il rapporto impulso/ pausa dell’onda quadra generata.

Chiude la serie di circuiti basilari la configurazione ‘monostabile’, cioè il tipico circuito di ritardo che viene utilizzato anche nei sistemi di automazione a logica sequenziale.

4) Risposta in frequenza degli amplificatori operazionali retroazionati.

La maggior parte dei libri di testo presenta il comportamento dei vari possibili modi di retroazione con la corrispondente funzione di trasferimento, cioè con l’espressione dell’operatore s di Laplace.

Questo è naturalmente corretto, ma richiede una capacità di astrazione matematica non comune, e sembra quindi preferibile un approccio che possa essere più intuitivo per la maggior parte degli studenti.

Il ricorso alla risposta in frequenza, nella forma di diagrammi di Bode, è certamente un modo per favorirne la comprensione (formalmente si tratta di sostituire jw all’operatore s e di trattare l’espressione come numero complesso, funzione della pulsazione w, riportandone l’andamento in diagrammi logaritmici).

Concettualmente l’interpretazione è elementare: il diagramma di Bode rappresenta l’andamento del rapporto fra segnale sinusoidale d’uscita rispetto quello, sempre sinusoidale, di ingresso, andamento in funzione della frequenza dei segnali (f = w/2p).

Una comprensione profonda del diagramma di Bode (che a rigore dovrebbe essere sempre completato con il diagramma delle fasi, spesso invece ignorato), fornisce quindi gli elementi sufficienti a prevedere il comportamento di qualsiasi configurazione, ed è questo che viene appunto illustrato nei programmi di questa serie di simulazioni (OAINDX).

Un’ulteriore segnalazione è che tali programmi, di più recente realizzazione, utilizzano i progressi fatti dai calcolatori negli ultimi anni, quali una maggior dimensione dello schermo e la possibilità di commenti audio, che facilitano ulteriormente la presentazione e la comprensione degli argomenti trattati.

Entrando più in dettaglio nei programmi di questa serie, si evidenzia la semplicità della risposta (costante al variare della frequenza) della configurazione proporzionale: è un altro modo di vedere la funzione delle moltiplicazione di un segnale per una costante, già incontrata all’inizio.

Questo però dà la possibilità di familiarizzarsi con l’interpretazione del diagramma di Bode (soprattutto con il guadagno in dB).

Più impegnativa è la comprensione della configurazione integratrice (con guadagno tendente all’infinito per frequenze tendenti a zero, cioè con segnali costanti): l’interpretazione della ‘pulsazione integrativa wi=1/RC’ (passaggio a 0 dB, cioè a guadagno =1), è fondamentale per afferrare l’essenza del comportamento dell’integratore, e la possibilità di far variare a piacere questo parametro (agendo sul valore di R), ne rende evidente il significato.

Così è anche per la configurazione derivatrice, duale della precedente, con il semplice scambio di posizione di R e C.

Di maggior importanza pratica è il caso della configurazione proporzionale-integrale (PI), in cui si devono considerare fondamentali i 2 parametri wi e wp: anche qui la possibilità di variazione dei parametri e l’immediato aggiornamento del relativo diagramma di Bode, rende intuitivo il legame fra le variazioni dei parametri e l’effetto sull’andamento della ‘risposta in frequenza’.

Per completezza, viene anche considerato il caso proporzionale-derivativo (PD). Anche se di minor importanza pratica, è interessante esaminare questo caso, soprattutto nella variante di limitazione dell’azione derivativa, in quanto propedeutica al più completo PID (che verrà dettagliatamente esaminato più avanti).

Termina questa serie invece la configurazione che simula il comportamento di una ‘costante di tempo’.

Questa configurazione può essere vista sia come un mezzo per simulare il comportamento di un sistema che viene posto in un anello di regolazione, sia come la forma più semplice di filtro passa-basso.

5) Esempi di applicazioni pratiche degli amplificatori operazionali retroazionati.

In questa serie ( APPINDX) vengono evidenziati i principali campi applicativi delle configurazioni finora viste.

Si inizia da un doppio filtro, un passa-alto e un passa-basso, entrambi a 2 stadi, con indicazione sia dei relativi diagrammi di Bode, sia dell’effetto che questi producono su un particolare segnale (50 Hz, con terza armonica).

Anche i programmi di questa serie sono illustrati da un commento audio, che guida alla comprensione e ne suggerisce l’utilizzo.

Mi limito quindi a citare qui l’esistenza dei programmi, senza entrare nei dettagli.

L’esempio dei filtri citato è importante per capire i fondamenti ma, come indicato, le prestazioni risultano piuttosto scarse, se non si ricorre ad altri tipi di configurazioni più complesse: i filtri a risonanza.

Il secondo caso esamina quindi i principi su cui si basano questi ultimi, per introdurre poi (terzo caso) i filtri cosiddetti ‘universali’.

La figura illustra il caso particolare del filtro universale in configurazione Passa Banda, con possibilità di selezionare i valori di frequenza centrale e di selettività (Q).

Si sottolinea comunque che la trattazione succinta di questi sia sufficiente a capirne l’essenza: una trattazione più particolareggiata come quella che si trova in ponderosi libri di testo, risulta del tutto inutile, vista la già citata tendenza dell’elettronica moderna alle soluzioni digitali (specialmente per i filtri), che si basano su tutt’altri principi e che garantiscono prestazioni nettamente superiori alle soluzioni analogiche, sia per precisione che stabilità.

Con lo stesso criterio vengono poi illustrate applicazioni di calcolo analogico (quarto e quinto caso), con lo scopo di far capire in che modo fosse possibile, prima dell’avvento dei calcolatori elettronici (almeno di quelli a basso costo), risolvere problemi anche complessi di automazione: soluzioni quindi ora obsolete, ma di notevole interesse concettuale.

6) Gli amplificatori operazionali nella regolazione automatica

Sempre riferendomi ai libri di testo in circolazione per l’insegnamento dell’elettronica, noto con una certa meraviglia che gran parte di questi si arresta davanti all’anello di regolazione.

Al massimo si citano i principi, si fa qualche esempio, ma non viene quasi mai affrontato il problema di progetto e verifica delle prestazioni di tale anello.

E’ un peccato, perché dopo tanto studio dei singoli elementi, non si arriva a quella conclusione che darebbe senso a tutto quanto: gran parte delle applicazioni è tuttora (malgrado la concorrenza digitale) basata sul classico regolatore analogico, il semplice ed economico PID.

Ma anche se fosse obsoleto, i suoi principi andrebbero comunque assimilati e non si potrebbero affrontare i ben più complicati regolatori digitali, senza queste basi.

Credo inoltre che sarebbe anche più gratificante per gli studenti vedere la conclusione pratica di quanto appreso: il progetto di un regolatore automatico.

A conclusione di questa panoramica di programmi di simulazione, vorrei quindi presentare l’ultima serie (oareg.exe) relativa appunto all’applicazione degli amplificatori operazionali nella regolazione automatica.

La simulazione riguarda sia il sistema regolato (a 1 o 2 costanti di tempo), sia il regolatore vero e proprio, che può essere di tipo PI, PD o PID, naturalmente chiusi ad anello.

Di questo programma vengono presentate due schermate (fig.1 e 2), per mostrarne la potenzialità di utilizzo (per gli altri non è stato qui fatto, perché avrebbe richiesto decine di figure).

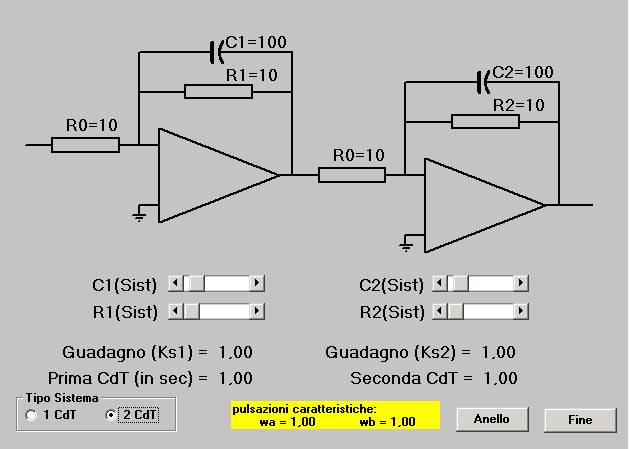
Schermata dal programma di simulazione degli amplificatori operazionali nella regolazione automatica: simulazione del sistema regolato (a 2 costanti di tempo).

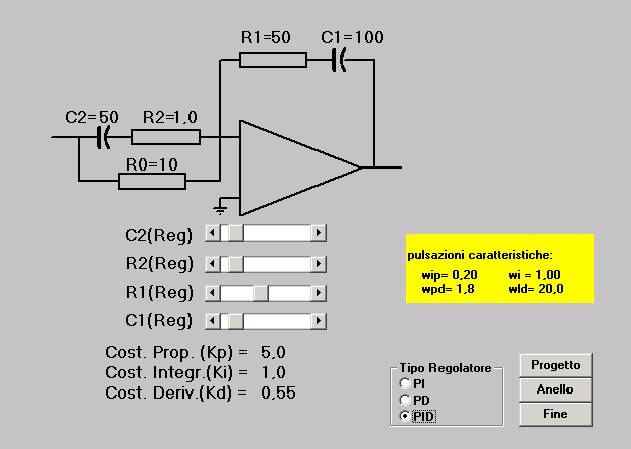
Schermata dal programma di simulazione degli amplificatori operazionali nella regolazione automatica: simulazione del regolatore (PID).

Le spiegazioni della Guida, contenuta nel programma stesso, dovrebbero essere sufficienti alla sua utilizzazione: in effetti si tratta di stabilire prima le costanti di tempo del sistema da regolare, di scegliere il tipo di regolatore e di determinarne i parametri.

Attivando poi il tasto ‘Bode’, si avrà la risposta (a ciclo aperto) dell’anello: da questo andamento si dovrebbero prevedere le prestazioni ottenibili con la effettiva chiusura dell’anello stesso (ed in questo consiste l’addestramento del progettista), prestazioni comunque verificabili con il tasto ‘gradino’ che applica all’ingresso dell’anello un riferimento a gradino, disegnando poi l’effettivo andamento nel tempo del segnale regolato (uscita).

La cosa non è però così semplice, ed ottenere un andamento dell’uscita non troppo oscillante e tuttavia nemmeno troppo lenta, è appunto l’arte del progettista (a meno di non ricorrere ai metodi di calcolo automatico dei parametri ottimi, disponibili nel programma stesso).

Credo (almeno mi auguro) che un po’ di esercitazioni su questa simulazione metta in grado chiunque perlomeno di capire il procedimento di messa a punto di un regolatore automatico, indispensabile premessa, come già detto, alla comprensione degli attuali ben più complessi regolatori digitali.