G. Schgör   (Sett. 2004)

 

Impiego del calcolatore per la soluzione di problemi logici

 

 

 

 

Sommario

Vengono presentati metodi di utilizzo dei calcolatori elettronici per ottenere i risultati finali da problemi risolvibili con l’algebra booleana.

Ovviamente la ‘traduzione’ dei problemi in espressioni booleane, cioè la parte concettuale della soluzione, non può essere svolta dal calcolatore, ma questo si rivela utilissimo per svolgere le operazioni algebriche altrimenti necessarie per giungere ai risultati, cioè la parte più noiosa ed a rischio di errori del procedimento.

Vengono dunque esaminati metodi  di utilizzo di Excel,  adatto ai  problemi più semplici, così come del VisualBasic per quelli più complessi.

Considerate però le possibili difficoltà di accesso ad ambienti di sviluppo speciali, anche se ampiamente diffusi, viene soprattutto presentato un  programma dedicato, sviluppato dall’Autore ed eseguibile in Windows,  che consente  un impiego semplice ed immediato.

 

 

Premessa

La  Logica Booleana  è da tempo  materia di studio nelle scuole italiane ma viene spesso trattata o come puro formalismo astratto ( ad es. nei Licei) oppure come sola base introduttiva agli elementi dell’elettronica digitale (negli Istituti Tecnici Industriali).

Risulta quindi  quasi del tutto ignorata l’applicazione  ‘pratica’  al ragionamento logico, come ad esempio è richiesto nella soluzione di problemi di deduzione da condizioni logiche stabilite  (spesso definiti significativamente ‘rompicapo’), e che è soprattutto di fondamentale importanza per la progettazione dei sempre più  complessi automatismi industriali.

 

 Tuttavia qualche segno incoraggiante in questo senso è recentemente apparso: l’esperimento didattico della  Professoressa Guarguaglini del  Liceo Scientifico  U. Dini di Pisa , riportato negli Atti del Convegno Didamatica 2004,  è un buon esempio di coinvolgimento degli studenti in questa materia.

 

In effetti si tratta di applicare i principi e le regole di questa particolare algebra che considera unicamente variabili a due soli possibili stati :  ‘VERO’ (1)  oppure   ‘FALSO’ (0).

Non essendo negli scopi di questo articolo richiamare concetti e regole di quest’algebra,  si rimanda ai relativi testi, segnalando però  anche l’esistenza di corsi gratuiti in Internet.

 

 

1)      Utilizzo di Excel

In particolare nel  mio Corso di  Algebra Booleana, disponibile appunto in Internet, dopo aver illustrato in modo essenzialmente intuitivo le basi concettuali e le operazioni logiche di quest’algebra, viene introdotta la possibilità di impiegare l’ambiente Excel per la compilazione delle tabelle di verità .

 

Il criterio seguito è molto semplice: ad ogni colonna del foglio Excel si fa corrispondere una particolare condizione logica e si combinano poi queste per ottenere nelle successive colonne espressioni più complesse, fino a quelle del risultato.

Questo sfrutta le funzioni logiche di Excel     E(...),  O(...),  NON(...),  che eseguono rispettivamente le operazioni logiche And , Or  e  Not, per elaborare le variabili e le loro combinazioni.

 

Nelle prime colonne si definiscono le variabili in gioco ed eventualmente le loro negazioni, per poi combinarle nelle successive colonne secondo l’espressione risolutiva del problema.

 

L’impossibilità in Excel di scrivere direttamente espressioni composte, comporta la necessità di procedere per gradi, definendo i singoli termini e componendoli poi in successive colonne.

 

Tralasciando qui la procedura, ovviamente illustrata in dettaglio nel corso citato, vediamo l’applicazione del metodo al seguente semplice problema logico:

 

 

 

 

Le note scritte nelle parentesi si riferiscono ad un ‘prontuario di traduzione’ riportato nel corso, con lo scopo di facilitare la scrittura delle espressioni  booleane corrispondenti alle singole condizioni del problema

 

Fig.1  -   Utilizzo di  Excel nella soluzione di un problema logico

 

 

La soluzione Excel, illustrata in fig.1, sta quindi nel preparare la tabella delle 4 variabili A,B,C e D ( e le singole colonne con i passaggi intermedi per ottenere prima notA (a), in colonna F,  e notC (c), in colonna G,  e poi singolarmente le  3  espressioni rispettivamente nelle colonne I,J,K.

Poiché le soluzioni richieste devono soddisfare tutte tre le condizioni, saranno valide solo le combinazione in cui in tutte tre queste colonne sono a  1, combinazioni evidenziate con  ‘OK’ in colonna L(istruzione: =SE(E(Ix;Jx;Kx);”OK”;””).

L’interpretazione di questi risultati è quindi facile, cioè  si può comperare:

solo C (riga 6)

B e C  (riga 8)

solo D (riga 10)

B e D  (riga 12)

A,B e D (riga 13)

C e D  (riga 14)

B,C e D (riga 16)

Quindi delle 16 possibilità di acquisto data dalle combinazioni delle 4 variabili, solo 7 risultano ammesse dalle condizioni del problema.

 

 

 

4)      Considerazioni didattiche

Dall’esempio appena visto, appare evidente che, al di là  delle difficoltà pratiche dell’uso di Excel, l’essenza del metodo è tutto basato sulla ‘traduzione’ del problema  in termini booleani, il che è estremamente formativo.

L’inevitabile equivocabilità del linguaggio nell’enunciato dei problemi si scontra con il rigore interpretativo delle espressioni logiche, ed è questo il primo punto importante.

Il secondo punto in ordine di importanza è l’equivalenza delle espressioni : mediante l’intuitivitá dei diagrammi di Venn deve essere  assimilato il significato profondo delle espressioni, evidenziando inoltre  le possibili equivalenze fra modi di scrittura formalmente diversi (fra cui anche le uguaglianze di DeMorgan).

 

Possiamo trarre esempi dal problema precedente.

La prima condizione  “se A allora B” sembrerebbe  esprimibile semplicemente con   (A and B), ma questo escluderebbe il caso in cui A sia falso (nel quale caso B potrebbe indifferentemente essere vera o falsa). Un’espressione più  completa è quindi   ((A and B) or not A), ma una rapida verifica  con il diagramma di Venn dimostrerebbe che l’A in and con B è ridondante, perciò l’espressione può essere ridotta  a  (notA or B), come indicato nell’esempio, pur mantenendone inalterato il contenuto logico.

Un altro approccio potrebbe essere la considerazione che l’unica cosa che  la condizione esprime è che non  deve essere  (A and notB), quindi   not(A and notB). Applicando DeMorgan possiamo verificare che quest’ultima espressione è equivalente alla precedente.

Così  la seconda condizione “non entrambi A e C”, può essere espressa come  not(A and C), che con DeMorgan diventa  (notA or notC), come indicato.

Nella terza condizione infine, si noti che   not(notC)  equivale a  C, quindi “se notC allora D” si può esprimere con  (C or D).

 

Deve essere pertanto ribadito il principio che è meglio concentrarsi sulla corretta impostazione del problema, lasciando al calcolatore l’onere di svolgere i successivi passaggi  algebrici, necessari per raggiungere i risultati.

La compilazione automatica delle ‘tabelle di verità’ da parte del calcolatore  rappresenta poi un grande aiuto per verificare l’effetto delle singole condizioni.

 

 

 

 

5)      Utilizzo di  Basic

L’impiego di un foglio elettronico come Excel è abbastanza semplice ed è anche pratico purché non si superi un certo grado di complessità.

La gestione di un foglio che  non sia tutto contenuto nelle dimensioni di una schermata, non è infatti così facile ed immediata, e se ne perdono quindi i vantaggi.

 

Per problemi più complessi, con elevato numero di variabili e soprattutto di condizioni, è consigliabile un diverso approccio, sfruttando le operazioni logiche possibili in ambiente Basic.

In particolare ci si riferisce qui al VisualBasic della Microsoft, che permette anche una facile gestione  nella visualizzazione dei risultati.

 

Il problema scelto per l’esemplificazione del metodo è tratto da un noto libro di passatempo logici, scritto quasi trent’anni fa da R. Smullyan, intitolato “Qual’è il titolo di questo libro?”.

In una serie di problemi di tipo poliziesco( nel capitolo “Dagli archivi dell’ispettore Craig”) vi è il seguente (n.76, pag 64):

In un’impresa criminale erano coinvolti 4 individui, A,B,C,D, e si erano riscontrati i seguenti fatti:  1)  A risultava innocente, ma il colpevole o i colpevoli, era sicuramente fra gli altri tre

2)      Se B era colpevole, aveva avuto un complice (uno solo)

3)      Se C era colpevole, aveva  avuto due complici.

L’ispettore Craig doveva stabilire se D era innocente o colpevole.

 

Il programma risolutore in Basic è riportato in fig.2, in cui si vede che le tre condizioni sono convertite in espressioni  logiche, in scrittura  standard, ed eseguite per tutte le combinazioni di A,B,C,D (loop For....Next).

Se  tutte le 3 condizioni risultano ‘Vere’ (-1, in Basic), viene stampata la corrispondente combinazione delle  4 variabili, che rappresenta appunto uno dei risultati.

 

Fig.2  -  Tipico programma in VisualBasic per la soluzione di un problema logico

 

 

La fig.3 riporta invece la schermata risultante dall’esecuzione del programma: dai fatti considerati risulta che oltre A,  anche C  è innocente, mentre D  è sicuramente colpevole. La posizione di B non è invece definita potendo essere o innocente o complice di D.

 

 

Fig.3  -  Risultato del programma  di fig.2.

 

Come si vede, anche l’utilizzo del Basic risulta semplice, ma ovviamente richiede la disponibilità di un apposito ambiente di sviluppo e, soprattutto, la capacità di programmare in questo linguaggio.

 

 

 

 

4) Programma SPL (Solutore Problemi Logici)

Dalle esperienze sopra citate, è scaturita l’idea di creare per la soluzione di problemi logici un programma dedicato, quindi indipendente da ambienti di sviluppo particolari, anche se ampiamente diffusi.

 

Tale programma è scritto in VisualBasic, ma convertito in forma eseguibile (SPL.exe) in modo da poter funzionare in normale ambiente Windows (il necessario programma interprete VBRUN300.dll è normalmente presente nelle varie versioni commerciali di questo software).

 

Caratteristica principale di questo programma è la semplicità d’uso: in una sola schermata possono essere risolti problemi da  2 a 4 variabili, con un massimo di  6 condizioni.

Le relative espressioni booleane possono essere impostate da tastiera , seguendo semplici convenzioni di scrittura, e la compilazione delle singole tabelle della verità avviene automaticamente all’attivazione del corrispondente  pulsante.

Un  ulteriore pulsante permette poi di evidenziare le soluzioni, cioè le combinazioni degli stati delle variabili che soddisfano tutte  le condizioni considerate.

 

Le convenzioni utilizzate per semplificare la scrittura delle espressioni sono illustrate nella ‘Guida’ contenuta nel programma stesso, ed essenzialmente si riducono alle seguenti:

 

- l'and fra variabili è sottinteso (es:  AB = A and B)

- la negazione di una variabile è rappresentata dalla corrispondente lettera minuscola (es: a = not A)

- l'or fra termini è rappresentato dal segno +  (es: A+B = A or B)

- la parentesi quadra [ ] rappresenta la negazione dell'espressione contenuta (es: [AB] = not(AB) )

- la parentesi tonda ( ) permette la raccolta dei termini comuni (es: A(B+C) = AB+AC )

 

 

La Guida riporta anche alcune limitazioni  nell’uso delle parentesi, ma dà  anche la possibilità di vedere alcuni esempi applicativi che dovrebbero rendere immediata  la comprensione delle procedure.

 

Iniziamo da un esempio estremamente semplice, con due sole variabili (A,B) ed una sola condizione.

Il problema considerato è lo stesso illustrato nell’esperimento didattico della  Professoressa Guarguaglini, già citato all’inizio ed è liberamente ricavato  dal capitolo ‘Cavalieri e Furfanti’ del libro di Smullyan, pure già citato.

Viene immaginata un’isola in cui vivono due sole specie di abitanti, indistinguibili fra loro, ma che hanno questa  caratteristica: gli uni (cavalieri) dicono sempre la verità, mentre gli altri (furfanti) mentono sempre.

Un esploratore che visita l’isola incontra due abitanti e chiede al primo:  “Voi due siete cavalieri o furfanti?”. Quello risponde: “io sono un furfante o lui è  un cavaliere”.

L’esploratore può stabilire la vera identità dei due?

 

Cominciamo assegnando al primo abitante la variabile A se cavaliere (quindi  a=notA,  se furfante) ed al secondo B se cavaliere (b se furfante). La risposta del primo può essere tradotta in  (a or B) e l’esploratore, sapendo delle caratteristiche degli abitanti, dovrebbe ragionare così: se chi ha risposto è un cavaliere quello che dice è vero, ma se è un furfante è vero il suo contrario.

L’espressione relativa, scritta con le convenzioni  sopracitate, è pertanto:     A(a+B)+a[a+B]

La fig.4 mostra appunto la schermata del programma in questo caso, con l’espressione scritta in R1 e supponendo di aver attivato il pulsante Cond.1, per ottenere la relativa tabella di verità.

Da quest’ultima risulta  ‘Vera’(=1) solo la combinazione AB (entrambi = 1), quindi si deve concludere che i due abitanti sono entrambi cavalieri.

 

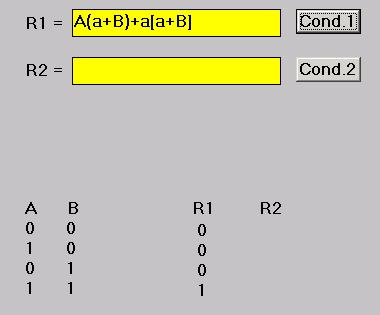
Fig.4  -   Esempio di utilizzo di SPL  nella soluzione di un problema logico a 2 variabili, con una sola espressione (particolare della schermata).

 

 

La conclusione può però lasciare perplessi: da un cavaliere ci si aspetterebbe ‘tutta la verità, nient’altro che la verità’ (come si recita nei tribunali), mentre la prima affermazione “io sono un furfante” risulta evidentemente falsa .  Come la mettiamo?  In realtà la risposta è vera nel suo complesso: con la ‘o’ si indica che almeno una delle affermazioni  è vera,  quindi la risposta  risulta corretta.

Paradossalmente anzi, se l’abitante avesse risposto ‘nient’altro che la verità’ cioè “siamo due cavalieri”, avrebbe messo in imbarazzo l’esploratore. Questo avrebbe dovuto infatti concludere che oltre alla possibilità  che i due fossero cavalieri, vi era anche la possibilità che  il primo fosse  un furfante, senza poter stabilire in questo caso l’identità del secondo.    

Infatti:                                            A(AB)+a[AB] =  AB + aB + ab

 

Disponendo del programma, è davvero semplice rendersi conto delle varie situazioni, potendo anche scrivere espressioni formalmente diverse nelle singole caselle (R1,R2,ecc.) e verificarne poi l’equivalenza o meno, con  i relativi pulsanti (Cond.1,Cond.2, ecc).

 

A conclusione di questa breve panoramica di utilizzo, si riporta in fig.5 lo stesso problema di Smullyan già visto risolto in Basic.

Si può osservare che, grazie alle convenzioni adottate, la scrittura e la comprensibilità delle espressioni  risulta più immediata rispetto alle stesse scritte in Basic.

 

I risultati (ottenuti col tasto Soluz. ed evidenziati  dall’incorniciatura) sono ovviamente gli stessi.

 

 

Fig.5  -   Soluzione in SPL dello stesso problema di fig.2  e 3 (schermata completa).

 

 

 

 

Conclusioni

Auspicando una maggior diffusione degli aspetti applicativi della Logica Booleana nelle Scuole italiane, intendo offrire come contributo a questa diffusione, l’utilizzo gratuito del programma SPL a tutti coloro che ne faranno richiesta via e-mail a:     g.schgor@polaris-net.it

Naturalmente sarò anche disponibile ad eventuali chiarimenti sulla sua applicazione.