G. Schgör - (Gen. 2005)
Esempi applicativi
della Logica Booleana
Sommario
L’articolo raccoglie gli esempi di applicazione delle proprietà e delle regole dell’algebra booleana a problemi logici di vario tipo.
L’argomento è stato trattato nel Forum del sito Internet: www.Matematicamente.it , dall’ottobre 2004 al gennaio 2005, con lo scopo appunto di divulgare l’applicazione ‘pratica’ di tale disciplina.
Si presuppone che la relativa teoria sia già nota, dando però anche riferimenti a corsi disponibili gratuitamente in Internet, fra cui:
- Corso di Logica Booleana (di G. Schgőr)
- Corso di Algebra Booleana (di A. Bobbio)
ai quali si rimanda per eventuali approfondimenti.
Gli esempi, dapprima elementari poi via via sempre più complessi, hanno, come si diceva, la funzione di introdurre l’effettiva utilizzazione di quest’algebra nella soluzione dei problemi logici, così come l’algebra convenzionale viene utilizzata nella soluzione di problemi numerici.
L’argomento non è futile, come qualcuno può pensare (poiché gli esempi sono più dei ‘rompicapo’ che dei problemi reali), ma al contrario, fortemente formativo di una mentalità più rigorosa, indispensabile per tutti coloro che dovranno affrontare la realizzazione di apparati sempre più ‘intelligenti’, cioè dotati di comportamenti automatici e autodiagnostici.
Gli esempi comunque sono in gran parte tratti da ricerche in Rete e da pubblicazioni specializzate (fra cui il noto libro di Smullyan “Qualè il titolo di questo libro?”), e le soluzioni sono ampliamente commentate, lasciando spazio alla riflessione dopo l’enunciazione dei singoli problemi.
Primo test
Iniziamo con un piccolo test sulla conoscenza della Logica.
Sapete spiegare perché le due seguenti frasi hanno diverso significato?
Attenzione. Non continuate se
non avete dato prima la risposta.
Siete d’accordo se al test precedente rispondo:
“ le due frasi sono diverse perché la prima esprime un 'Nand' ( not(A and B) ) fra le variabili A (Anna suona) e B (Bice canta), mentre la seconda esprime un 'Nor' ( not(A or B) ) fra le stesse variabili”.
E se rispondo:
“le due frasi sono diverse perché la prima esprime un 'or' delle negazioni ( (not A) or (not B) ) e la seconda un 'and' delle stesse negazioni ( (not A) and (not B) ) “.
siete ancora d’accordo?
Se non siete pienamente convinti che due precedenti risposte sono equivalenti, consiglio un approfondimento delle proprietà booleane (in particolare sulle uguaglianze di DeMorgan), consultando i corsi in Internet indicati, prima di affrontare i prossimi problemi.
Primo problema logico.
Ma se avete deciso di proseguire, ecco subito un problemino.
Date le affermazioni
1) Se Anna suona, Bice canta
2) Se Bice non canta, Carla
studia
3) Anna non suona e Carla non
studia
si chiede: Bice canta o no?.
Attenzione. Non continuate se
non avete dato prima la risposta.
La risposta è: Bice canta.
Ma vediamo in dettaglio l’applicazione del procedimento booleano.
Innanzitutto dobbiamo trasformare le condizioni in equivalenti espressioni
logiche delle 3 variabili A (Anna suona), B (Bice canta) e C (Carla studia).
La prima affermazione può essere
tradotta in: (not A) or B
La seconda in: B
or C
La
terza in: (not A) and (not C)
La soluzione, dovendo soddisfare tutte le 3 condizioni, deve essere il
prodotto logico delle 3 espressioni, e risulta (not A) and B and (not C) (le altre 7 combinazioni delle 3 variabili, risultano infatti
tutte ‘False’).
L’interpretazione è quindi che l’unica situazione ammessa è quella in cui:
Anna non suona, Bice canta e Carla non studia.
Vorrei però aggiungere che il procedimento può essere ulteriormente semplificato mediante l’impiego di un calcolatore elettronico
Allo stesso modo in cui un problema numerico può essere risolto facendo
svolgere i calcoli relativi appunto ad un calcolatore, si può ricorrere a
quest’ultimo per svolgere le operazioni logiche che portano alla soluzione
(cioè il prodotto logico delle 3 espressioni).
Si sottolinea che la pura esecuzione dei calcoli non rappresenta mai la parte
concettualmente più importante della soluzione, ma che richiede soltanto
un’attenta esecuzione di regole, il che è compito ideale per un calcolatore.
Fra i diversi possibili modi di utilizzare questo strumento per tale scopo, vorrei
segnalare un programma che è stato sviluppato appositamente per la soluzione di
problemi logici, e che può essere prelevato da Internet attivando il programma SPL (Solutore di Problemi
Logici) .
Come per tutti gli ambienti di calcolo, la sua utilizzazione richiede
l’accettazione di convenzioni nella scrittura delle espressioni booleane da elaborare,
convenzioni illustrate nella ‘Guida’
del programma stesso e che seguono quanto è normalmente adottato nella pratica
applicazione di questa logica.
Essenzialmente il prodotto logico fra variabili (and) viene sottinteso
(cioè AB = A and B) e la somma logica (or) viene rappresentata dal segno +
(cioè A+B = A or B).
Per la negazione (not) nella pratica si ricorre ad una lineetta sopra la
variabile, ma questo è piuttosto scomodo da realizzare col calcolatore, perciò
viene qui adottato il criterio di scrivere la variabile in minuscolo (cioè a = not A).
Con queste semplici convenzioni, possiamo ora adoperare il programma scrivendo nelle apposite caselle le espressioni del nostro problema:
R1 = a+B
R2 = B+C
R3 = ac
Attivando i tasti a lato di ciascuna espressione, otterremo le singole tabelle
di verità corrispondenti (1 = Vero, 0 = Falso), ed alla fine, attivando il
pulsante ‘Soluz.’, otterremo l’evidenziazione del risultato.

Come si vede, il risultato evidenziato dal riquadro è: A=0 (Anna non suona), B=1 (Bice canta) ,
C=0 (Carla non studia)
Il problema degli aperitivi
Nei links del sito Internet di Matematicamente, vi è anche quello di Logica e Fondamenti con un ottimo corso del prof. A. Maida.
Sebbene tale corso sia essenzialmente teorico ed orientato ad illustrare i fondamenti logici della matematica, vi è riportato un esempio di problema logico che mi permetto di riportare qui:
1) Se A prende l'aperitivo, allora lo prende anche B
2) B e C prendono l'aperitivo,
ma non assieme
3) A o C prendono l'aperitivo
4) Se C prende l'aperitivo,
allora lo prende anche A
Si chiede chi dei tre (A,B,C) prende
l'aperitivo e chi no.
Attenzione. Non continuate se non avete dato prima la risposta.
Come primo passo occorre “tradurre” le singole condizioni del problema in altrettante espressioni booleane, in termini di sole operazioni primarie (not, and, or).
1) Se A prende l'aperitivo,
allora lo prende anche B -> (not A) or B
2) B e C prendono l'aperitivo,
ma non assieme -> (B and (not C)) or (C and (not B))
3) A o C prendono
l'aperitivo -> A or C
4) Se C prende l'aperitivo,
allora lo prende anche A -> (not C) or A
(si osservi che non è sempre semplice interpretare l’effettivo significato
logico delle frasi, come ad es. la 2, che pur usando una “e”, in realtà
comporta un or esclusivo).
Si sottolinea che questa è l’unica fase concettualmente impegnativa, paragonabile all’impostazione delle equazioni in un problema numerico.
Il resto è una pura applicazione di regole, e può essere quindi risolto, come vedremo, dal calcolatore.
La soluzione si ricava infatti facendo il prodotto logico (and) di tutte le
condizioni imposte. cioè, ricorrendo
alle convenzioni proposte, si devono eseguire i prodotti logici: (a+B)(Bc+bC)(A+C)(c+A)
Applicando le proprietà dell’algebra booleana, si ricavano 16 termini,di cui
però, in questo problema, solo uno risulta diverso da zero (cioè non è un
insieme vuoto).
Questo termine è ABc , e che significa che A e B prendono l'aperitivo, ma non C
Come si vede, il procedimento è elementare e fornisce con sicurezza tutte le
possibili soluzioni, (se non si commettono errori nello sviluppo algebrico!).
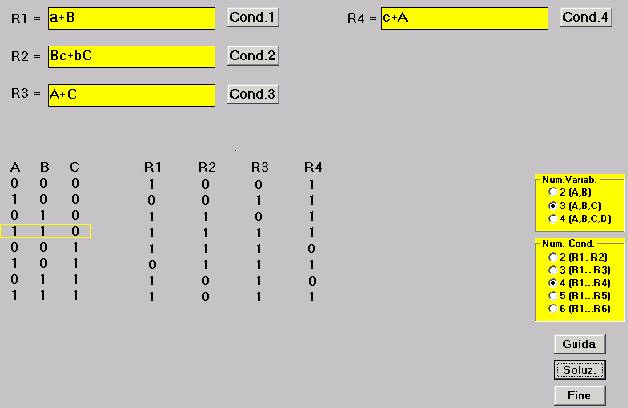
Per evitare questi possibili errori, si può ricorrere al calcolatore, cioè al programma SPL già citato.
Scrivendo le singole espressioni logiche negli appositi riquadri (R1…..R4) si ottengono le relative tabelle di verità per ciascuna condizione, quindi il risultato in corrispondenza della riga in cui tutte queste tabelle sono =1.
L’isola dei cavalieri e dei
furfanti
Una delle fonti più note di problemi logici è il libro di Raymond. Smullyan dallo strano titolo “Qual’è il titolo di questo libro?”, scritto una trentina di anni fa e che raccoglie ben 270 rompicapo.
Mentre l’autore (professore di Logica in Università americane) dà la soluzione di ogni problema con complicati ragionamenti deduttivi, si vuole qui dimostrare che l’applicazione dell’algebra booleana consente di ottenere le stesse soluzioni in modo semplice e rapido (soprattutto se facilitato dall’uso del calcolatore).
La fertile fantasia di Smullyan ha immaginato l’esistenza di un’isola su cui vivono solo due sole specie di abitanti, indistinguibili fra loro, ma che hanno questa caratteristica: gli uni (cavalieri) dicono sempre la verità, mentre gli altri (furfanti) mentono sempre.
Un esploratore che visita l’isola incontra degli abitanti e pone loro delle domande per identificarli.
Dalle domande e soprattutto dalle loro risposte, nasce tutta una serie di problemi logici di più o meno difficile soluzione.
Cominciamo da uno dei più semplici.
Supponiamo che l’esploratore incontri due abitanti e chieda loro “siete cavalieri o furfanti?” e che il primo risponda “io sono un furfante, ma lui non lo è ”
(problema n. 33, a pag. 22).
L’esploratore può stabilire chi è cavaliere e chi furfante?
Per chiarezza, diciamo che in base alle premesse, un furfante è (booleanamente parlando) un non-cavaliere e che le risposte sono “vere” se le dà un cavaliere, ma se a darle è un furfante la verità è esattamente il contrario della risposta stessa.
Per convenzione, è opportuno poi indicare il primo abitante (quello che in questo caso dà la risposta) con A se cavaliere (e quindi a = not A , se furfante), ed il secondo rispettivamente
con B, (se cavaliere ) oppure b (se furfante).
Attenzione. Non continuate se
non avete dato prima la risposta.
Il ragionamento che l’esploratore deve fare, date le premesse del problema, è che se chi dà la risposta è un cavaliere (quindi A), allora la sua risposta è vera ma, in caso contrario (quindi a, se cioè è un furfante), la verità è esattamente il contrario della risposta.
L’espressione booleana corrispondente a questa situazione è quindi :
(A
and (risposta)) or (a and not(risposta)) .
Tale struttura di espressione vale per qualsiasi risposta che l’interpellato dà (ovviamente tradotta in termini booleani).
La risposta “io sono un furfante ma lui non lo è” è facilmente ‘traducibile’ in: (a and B) .
L’intera espressione, adottando le convenzioni proposte, risulta quindi: A(aB)+a[aB].
Procedendo algebricamente, si
nota che il primo termine è nullo
(Aa=0), mentre il secondo (con un Nand rappresentato dalla parentesi
quadra) deve essere sviluppato applicando DeMorgan in: a(A+b), quindi = ab
L’interpretazione del risultato è che i due sono entrambi furfanti.
Con il programma SPL, la soluzione è immediata dopo aver scritto l’espressione nel campo R1: l’attivazione del pulsante laterale (Cond.1), mostra la tabella con una sola condizione vera (=1) in corrispondenza di A=0 e B=0, il che significa che sono veri sia a che b.
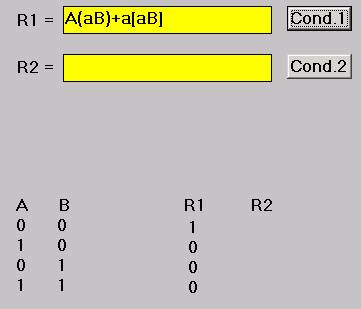
Per dimostrare che il procedimento illustrato non è una perdita di tempo, ma una reale facilitazione, propongo la soluzione di 3 altre possibili risposte che l’interpellato avrebbe potuto dare.
Quindi, medesime premesse, ma differenti situazioni.
Risp.1 “Almeno uno di noi e’ un furfante”
Risp.2 “Siamo due furfanti”
Risp.3 “Io sono un furfante o lui e’ un cavaliere”
Attenzione. Non continuate se
non avete dato prima le risposte.
Le soluzioni dei casi precedenti sono facilmente ottenibili seguendo la struttura dell’espressione
logica indicata , e ponendo le singole risposte in termini booleani.
Risp.1: “Almeno uno di noi è un furfante” -> a+b
Risp.2: “Siamo due furfanti” -> ab
Risp.3: “Io sono un furfante o lui è un cavaliere” -> a+B
Quindi le espressioni risolventi sono rispettivamente:
R1 = A(a+b)+a[a+b]
R2 = A(ab)+a[ab]
R3 = A(a+B)+a[a+B]
Con il programma SPL si ottengono poi le soluzioni:
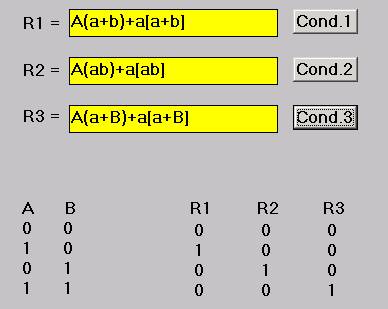
R1 = Ab (il
primo è un cavaliere, l’altro un furfante)
R2 = aB (il primo
è un furfante, l’altro un cavaliere)
R3 =AB (sono entrambi cavalieri)
Mentre questi casi danno per ciascuno una sola soluzione, è evidente che ci possono essere risposte che ammettono più alternative.
Fra queste c’e’ il problema di Smullyan n.29 (pag.21), in cui la risposta del primo è:
“io sono un
furfante o, in alternativa, lui è un cavaliere”.
A dire il vero, Smullyan dà una sola soluzione (lunga un’intera pagina), e mi sono alquanto sorpreso quando, applicando l’SPL, ho ottenuto una seconda possibile soluzione.
Ma mi sono reso conto che il calcolatore ….aveva ragione!
Sapete trovare (e giustificare) le due soluzioni?
Attenzione. Non continuate se
non avete dato prima le risposte.
Le soluzioni dell’ultimo problema sono ottenibili considerando che la risposta dell’ abitante è un
“or-esclusivo” (a xor B), equivalente all’espressione (ab+AB).
Messa nella solita struttura, comune a tutti questi problemi, si ottiene: A(ab+AB)+a[ab+AB]
che risolta dà: AB (entrambi gli abitanti sono cavalieri), ma anche aB
(il primo è un furfante, il secondo un
cavaliere).
Ma quest’ultima situazione corrisponde alle due affermazioni che fa il primo (“io sono un furfante”
“lui e’ un cavaliere”), quindi come può essere un furfante se dice cose vere?
In realtà la risposta è falsa nel suo complesso poiché, dando le due situazioni in alternativa, esclude proprio che possano essere vere entrambe, quindi chi la dà è un furfante.
Più esattamente, la soluzione algebrica di questo problema è semplicemente = B , cioè solo per il secondo abitante si può stabilirne l’identità (è un cavaliere) mentre rimane indeterminata l’identità del primo.
La possibilità di soluzioni multiple ovviamente si riduce se vi sono più risposte da parte degli abitanti, ma è evidente che l’analisi si complica, facendo risaltare i vantaggi di seguire il metodo algebrico, rispetto all’analisi deduttiva diretta.
Ecco un problema con 3 abitanti e con 2 risposte (n.31, pag.21).
Per maggior chiarezza, chiamiamo A il primo abitante, B il secondo, C il terzo, con la convenzione che A=1 se cavaliere (quindi A=0, ovvero a=(not A)=1, se furfante), e così per gli altri.
Allora, stessa domanda da parte dell’esploratore (“siete cavalieri o furfanti?”), e in questo caso
A risponde: “siamo tutti furfanti”, mentre
B risponde: “solo uno di noi è un cavaliere”
Chi è cavaliere e chi furfante?.
Attenzione. Non continuate se
non avete dato prima la risposta.
La risposta di A (“siamo tutti furfanti”) è facilmente convertibile in abc .
La risposta di B (“solo
uno di noi è un cavaliere”) si può invece esprimere come somma logica delle possibili
combinazioni: Abc+aBc+abC
(solo il primo è un cavaliere e gli altri 2 sono furfanti, oppure solo
il secondo è un cavaliere………… ecc.).
Essendo due le risposte, la struttura dell’espressione risolvente sarà il prodotto logico delle due condizioni (devono essere ‘vere’ entrambe):
R1 = A(abc)+a[abc]
R2 = B(Abc+aBc+abC)+b[Abc+aBc+abC]
Come si vede, la soluzione ‘algebrica’ del prodotto delle due, pur essendo fattibile, risulta piuttosto noiosa da svolgere (ma soprattutto c’è il pericolo di commettere errori banali).
Per questo si consiglia l’uso del programma SPL.

(purtroppo le dimensioni del campo di R2 non consentono di mostrare l’intera espressione, che però è quella indicata più sopra)
La soluzione, immediata, è: aBc (solo il secondo è un cavaliere, gli altri 2 sono furfanti).
Credo che a questo punto sia superfluo continuare con gli esempi di questo tipo, rimandando al libro di Smullyan chi trovasse interessante proseguire.
Del resto chiunque potrebbe ‘inventare’ casi con più abitanti e più risposte, constatando che con un approccio tradizionale di deduzione logica diventerebbe sempre più arduo arrivare a soluzioni certe e, soprattutto, complete.
I casi dell’ispettore Craig
Sempre citando il libro di Smullyan, fra i molti argomenti affrontati dall’autore, ho trovato di particolare interesse quelli relativi ai casi polizieschi (capitolo 6 – Dagli archivi dell’ispettore Craig).
Ne riporto qui solo un paio.
Il primo caso (probl. 78, pag. 64) si riferisce al processo di tre uomini (A,B,C) accusati di furto.
I fatti accertati sono:
1)
Se A è
innocente o B è colpevole, allora C è
colpevole
2)
Se A è innocente,
allora C è innocente
Si può stabilire per ognuno dei tre se è colpevole o innocente?
Stabilendo la convenzione di indicare con le lettere maiuscole lo stato d’innocenza (quindi con le minuscole lo stato di colpevolezza), il primo fatto si può convertire nell’espressione: [A+b]+c
(ricordiamo che ‘se X, allora Y’ corrisponde a ( not X) or Y ), ed il secondo in: a+C .

Il programma solutore (SPL) mostra che A è sicuramente colpevole (A=0, quindi a=1, colpevole),
mentre per gli altri due non può essere stabilito né lo stato di innocenza, né quello di colpevolezza.
Il secondo caso (probl. 80, pag.65) gli imputati sono 4 ed i fatti sono i seguenti:
1)
Se A e B sono entrambi colpevoli, allora C fu loro
complice
2)
Se A è colpevole, almeno uno, tra B e C, fu suo
complice
3)
Se C è colpevole, allora D fu suo complice
4)
Se A è innocente, allora D è colpevole
Quali sono gli imputati sicuramente colpevoli e per quali esistono invece dei dubbi?
Attenzione. Non continuate se
non avete dato prima le risposte.
La conversione per ciascun fatto e con le stesse convenzioni adottate, è:
1) Se A e
B sono entrambi colpevoli, allora C fu loro complice -> [ab]+c
2) Se A è
colpevole, almeno uno, tra B e C, fu suo complice -> a(b+c)+A
3) Se C è
colpevole, allora D fu suo complice ->
d+C
4) Se A è
innocente, allora D è colpevole
->
d+a
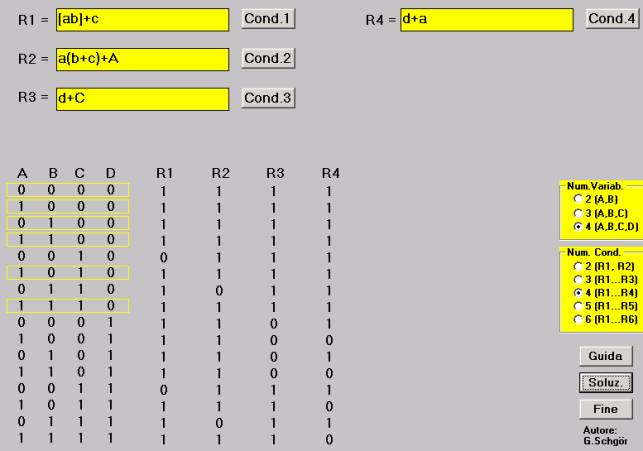
Le soluzioni (nei riquadri gialli) dimostrano che solo D è sicuramente colpevole (D=0, cioè d=1).
Per gli altri tre non è possibile stabilire (almeno dai fatti considerati) alcun giudizio.
Sarebbe interessante studiare come varianti aggiuntive le possibili prove che gli avvocati difensori degli altri imputati potrebbero portare per scagionare i loro clienti (per es. se l’avvocato di A dimostrasse che il suo assistito non poteva essere complice di C, A risulterebbe sicuramente innocente).
Ritengo, con questi esempi, di aver chiarito le potenzialità di utilizzo del metodo booleano e l’utilità del programma solutore (SPL) anche in questo tipo di argomenti.
Rimando ovviamente al libro di Smullyan per tutti gli altri numerosissimi casi a cui il metodo qui seguito potrebbe essere applicato.
Vorrei però concludere questa panoramica di applicazioni con una considerazione sull’importanza di questa metodologia che, almeno a quanto mi risulta, non è per niente diffusa nelle scuole italiane.
Un problema di progetto
Per evitare l’impressione che questa metodologia sia applicabile solo a giochetti rompicapo, e non a problemi pratici reali, vorrei concludere la serie di esempi con un problema che potrebbe presentarsi in un progetto di automatismo.
Supponiamo che il comando di attivazione di una certa azione sia determinato dallo stato di 4 segnali (A,B,C,D, ciascuno dei quali può assumere solo 2 stati: “1”, oppure”0”), e che la ‘specifica’ di progetto (cioè la descrizione delle condizioni di funzionamento desiderate) sia quella qui sotto riportata.
Il comando di attivazione (R) deve avvenire quando si presentano entrambe le seguenti condizioni:
1) con
C=0 e quando A o B sono =0
2) con B e C =1,
oppure con D=1
ed A=0
Un progettista poco esperto, prendendo alla lettera la specifica, concluderebbe che ci vogliono almeno 6 operazioni logiche (quindi 6 elementi circuitali elementari di tipo ‘or’ o ‘and’) per ottenere il segnale R dai 4 di ingresso (supponendo di disporre già anche gli equivalenti negati).
Orbene, con un po’ di algebra booleana si dimostra che l’intera configurazione si può ridurre ad un solo elemento logico (per giunta a 3 ingressi, essendo indifferente lo stato di uno dei 4 segnali), invece dei 6 ritenuti necessari.
Credo a questo punto di poter lasciare al lettore la soluzione (che può essere ulteriormente facilitata dall’impiego del programma SPL).
Lasciatemi però sottolineare, con grande rincrescimento, che il mancato interesse dimostrato nel Forum dalla maggioranza dei futuri ingegneri verso questi argomenti (solo pochi giovanissimi hanno partecipato), non sembra incoraggiare all’ottimismo sul ruolo dell’industria italiana nei settori produttivi più avanzati.