G.  Schgör   (Ott.  2005)

 

Algoritmi  semplici per assonometria e prospettiva

 

 

Sommario

Viene affrontato il problema di rappresentazione grafica di una figura tridimensionale su un piano di proiezione (schermo video), considerando sia il metodo assonometrico, sia quello più complesso della prospettiva.

Si vogliono cioè determinare  algoritmi che consentano ad un programmatore di grafica con computer di passare da uno spazio tridimensionale alla sua proiezione piana con regole sufficientemente semplici, tali comunque da non richiedere speciali strumenti di calcolo che non siano già previsti nei normali linguaggi di programmazione.

 

Vengono perciò indicate procedure semplificate, adatte alla rappresentazione grafica di figure elementari, quali quelle utilizzate per  illustrazioni didattiche, dandone anche esempi applicativi.

 

 

 

Rappresentazione assonometrica

Un punto nello spazio tridimensionale è  definito da una terna di coordinate riferite ad una terna di assi (x,y,z) fra loro perpendicolari (rappresentazione “cartesiana”).

Una volta definito il centro (o “origine”) degli assi e la direzione di questi, un generico punto  p  è  infatti individuato dalla sua distanza  nella direzione di ciascun asse. Le coordinate del punto xp.yp,zp sono quindi le rispettive distanze, espresse in una appropriata unità di misura.

 

Questo è semplice da capire, ma quando lo si voglia illustrare su un piano (un foglio di carta o lo schermo video) sorge una complicazione: la mancanza della terza dimensione!

Si può ovviare a questo, rappresentando il terzo asse (quello che uscirebbe perpendicolarmente dal

piano di disegno) con una retta giacente nel piano, ma obliqua rispetto alle altre due.

 

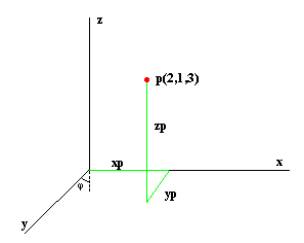
La figura illustra chiaramente questo principio, mostrando l’asse y  inclinato di un angolo  j  rispetto alla verticale. E’ questa una delle forme più comuni di  assonometria,  in cui  la terna di coordinate  del punto (xp,yp,zp) viene ridotta  alle due coordinate  di  proiezione sul piano zx, rispettivamente  xpp e zpp.

Queste due sono ricavate facilmente dalle relazioni:  xpp = xp - yp*sen(j)   e  zpp = zp - yp*cos(j).

 

E’ quindi ovvio che definendo una qualsiasi figura mediante le coordinate dei suoi singoli punti, è possibile convertirla in rappresentazione piana semplicemente applicando queste relazioni (e per un calcolatore è un’operazione banale).

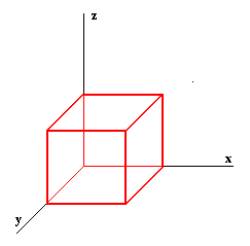
La figura mostra la rappresentazione di un cubo (8 vertici, quindi altrettanti punti  da  calcolare e poi da congiungere con segmenti di retta).

Si noti che per dare maggior  realismo alla  figura, si è introdotto una unità di misura diversa per l’asse y (i 2/3 dell’unità di x e z). Anche con questo accorgimento si nota una forma che non soddisfa pienamente le regole della normale visione tridimensionale: il  mantenimento del parallelismo degli spigoli contrasta infatti con l’impressione di convergenza con la profondità che si ha nella realtà (vedremo il superamento di questo con la prospettiva).

 

Particolarmente interessante è la rappresentazione assonometrica di curve spaziali (qualora se ne sappia esprimere matematicamente l’equazione). Più problematica è la rappresentazione di superfici, per cui per poterne interpretare l’andamento, occorre prevedere un disegno a strati (curve di livello) o a  reticolo.

 

Un’osservazione importante per il disegno mediante calcolatore di curve o superfici spaziali è che spesso è opportuno ricorrere ad una rappresentazione in coordinate “polari”, anziché cartesiane. Questo consente di spaziare più uniformemente i punti calcolati, quindi di ottenere un migliore aspetto.

 

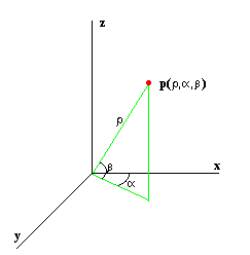
La figura illustra  la convenzione solitamente adottata per  esprimere la “posizione” del generico punto p in coordinate polari.

Si deve sottolineare che la conversione tra i due tipi di coordinate è elementare (ovviamente per un calcolatore) e si basa sulle seguenti relazioni:

 

da cartesiane a polari:

r = Ö(xp^2+yp^2+zp^2)

b = arcsen(zp/r)

a = arcsen(yp /(r*cosb)

 

da polari a cartesiane:

xp = r*cosa*cosb

yp = r*cosa*senb

zp = r*senb

 

Ecco ad esempio come può essere disegnato uno spicchio di sfera (1/8) con centro coincidente con l’origine degli assi.

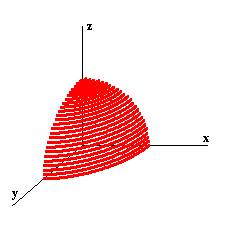
L’equazione è    x^2+y^2+z^2=R^2 , che può essere prima convertita in coordinate polari, utilizzando poi queste per calcolare i singoli punti da disegnare. Ovviamente  r=R e, tenendo costante  b, si può far variare  a con incrementi costanti da 0 a 90° (se tali incrementi sono sufficientemente piccoli si otterrà una linea continua anziché i singoli punti).. Incrementando poi  b, si potrà disegnare un secondo “strato”, e così via.

 

Il metodo illustrato è particolarmente adatto a rappresentare soluzioni di problemi di geometria  tridimensionale.

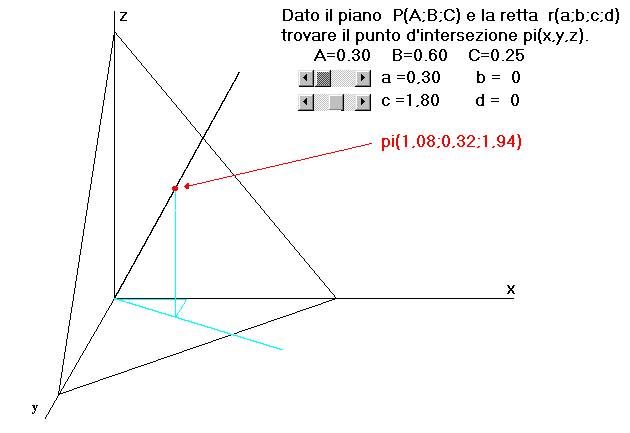
La figura che segue mostra la presentazione grafica di un programma che calcola il punto di intersezione di un piano con una retta.

 

L’equazione canonica di un piano P(A,B,C) è data da  A*x+B*y+C*z=1 (si osservi che A,B,C sono gli inversi delle intercette con i rispettivi assi) mentre la retta r(a,b,c,d) è definita dalle sue proiezioni sui piani xy (y=a*x+b)   e   zx (z=c*x+d).

Il programma (in Visual Basic) calcola  il punto di intersezione pi(x,y,z) e ne dà la rappresentazione grafica, partendo da dati prefissati (variabili nel programma) e dai due parametri a e c variabili mediante cursori ( per semplicità si sono posti =0 i parametri b e d, cioè facendo passare la retta per l’origine degli assi): ogni volta che si cambia   a o c , viene ridisegnata la figura con il nuovo punto d’intersezione.

Questo rende molto più intuitiva la soluzione, con l’immagine immediata (il che non è poi così facile da immaginare in uno spazio tridimensionale).

 

 

Come ultimo esempio di rappresentazione assonometrica,  cito la soluzione grafica di uno dei problemi posti nella “Gara di Matematica” del sito matematicament.it.

 

Il problema chiedeva  di determinare la direzione di lancio di una bilia in un ideale “biliardo tridimensionale” (a parallelepipedo ed in assenza di gravità) in modo tale che, lanciata da un  punto qualsiasi di una faccia, la bilia tornasse allo stesso punto di partenza dopo aver  rimbalzato su tutte le altre facce.

Le traiettorie relative alla soluzione sono ottenibili richiamando il programma:

http://www.matematicamente.it/giochi/biliardo3d_sol5.exe

ed attivando il tasto di simulazione.

Il programma (in edizione eseguibile di Visual Basic) richiede per l’esecuzione l’interprete VBRUN300.dll (qualora non già disponibile, scaricabile da: http://matfisinf.supereva.it/VBRUN300.DLL )

 

Agendo sui cursori, è possibile variare a piacere il punto di partenza e verificare il ritorno della bilia in questo punto.

Dal punto di vista grafico, si noti l’opportunità di indicare anche la proiezione delle traiettorie sulla faccia orizzontale inferiore, per meglio mettere in risalto la tridimensionalità di queste.

 

 

 

 

 

 

 

 

 

Prospettiva

Si è già accennato al fatto che la rappresentazione assonometrica non riproduce gli effetti della visione tridimensionale, che rimpicciolisce gli oggetti più distanti dall’osservatore.

Il problema, che ha interessato la pittura per centinaia di anni, è stato ormai risolto con le regole della prospettiva.

Normalmente questo viene ottenuto con procedure grafiche che, dato il disegno in scala degli oggetti nelle direzioni frontale, laterale e dall’alto (cioè “in pianta”), permette di ottenere una visione “panoramica” tridimensionale.

Poiché lo scopo è qui di dare al programmatore di grafica computerizzata uno strumento matematico che gli permetta di fare la stessa cosa, dobbiamo trasformare le coordinate di un generico punto p, individuato rispettivamente da  xp,yp,zp, in una coppia di coordinate (xpp,zpp) sul piano do proiezione.

Per semplificare questa trasformazione, assumiamo come piano di proiezione lo stesso piano zx e supponiamo che la posizione dell’osservatore sia nel piano yz  (con altezza HO  e distanza DO dal centro degli assi).

 

Date quindi le coordinate del punto nello spazio x,y,z, è elementare ricavare geometricamente le espressioni delle coordinate x e z della sua proiezione sul piano zx  (è l’intersezione della retta passante per p e per l’osservatore, con il piano zx, cioè y=0).

 

Risulta:   xpp =xp/(1+yp/DO)    e    zpp=(zp*DO + yp*HO) /(yp+DO)

 

E’ interessante notare che il piano orizzontale passante per l’osservatore (z=HO) interseca il piano di proiezione xz formando quella che viene chiamata “linea di orizzonte”. Su questa giacciono i punti di fuga, cioè quei punti a cui convergono le rette corrispondenti alle parallele nel disegno tridimensionale.

 

Vediamone un’applicazione rappresentando uno spigolo di parallelepipedo con due sole facce visibili.

 

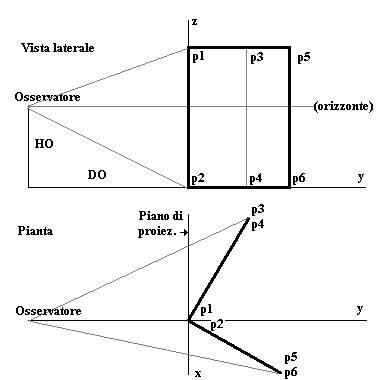
Date la vista laterale e la pianta (che individuano così l’oggetto da proiettare) si possono ricavare le coordinate sui tre assi (x,y,z) dei sei punti (p1…p6) da trasformare in rispettive coordinate  xpp,zpp sul piano di proiezione (zx).

Il risultato è la rappresentazione in prospettiva:

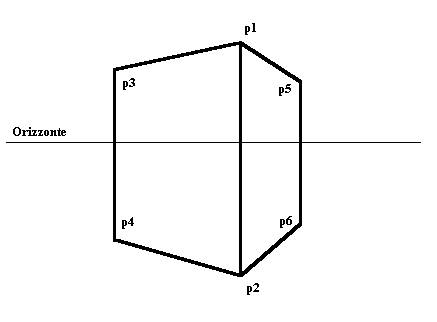
Come si vede, le parallele p1- p3  e  p2-p4  dell’oggetto originale, convergono ora verso un punto dell’orizzonte (che può essere determinato dall’intersezione dalla retta orizzontale  dall’osservatore e  parallela al lato di sinistra, con il piano di proiezione). Lo stesso si può dire per il lato di destra. Questi punti di convergenza sono detti punti di fuga e corrispondono alla posizione che si avrebbe se ciascun lato si prolungasse all’infinito.

 

 

Si fa notare che il metodo è applicabile anche a  forme curve (solitamente di laboriosa e difficile procedura se la proiezione  è eseguita geometricamente). Ovviamente vanno calcolati  molti più punti, ma se la curva è esprimibile in forma matematica, questo non è un problema.

 

Come esempio di  questo, ecco la prospettiva di un arco (semicerchio), disegnato sul lato destro dello stesso parallelepipedo visto prima..

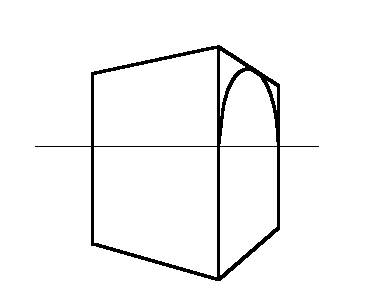
Si  fa notare che la rappresentazione di archi su piani verticali, inclinati sul piano di proiezione (zx) di un angolo  g, è  semplicemente espressa da

xp = xc – R*cos(g)*cos(d)

yp = yc – R*sen(g)*cos(d)

zp = zc – R* sen(d )

dove (xc,yc,zc) sono le coordinate del centro dell’arco, R il suo raggio e d l’angolo al centro, che va incrementato da  0  a  p/2  per tracciare il semicerchio.

Ovviamente, ciascun punto così calcolato va “proiettato” sul piano zx con le formule di trasformazione date, per ricavarne le coordinate xpp e zpp del corrispondente punto da tracciare.

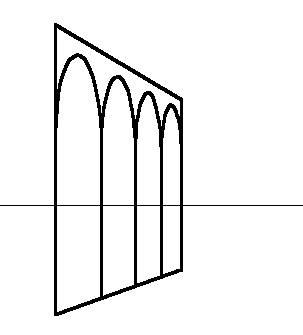
La figura mostra  il risultato di 4 archi uguali e consecutivi su un piano verticale, tracciato con le formule precedenti, semplicemente cambiando per ciascuno la posizione del rispettivo centro.

 

 

 

Conclusioni

Si è mostrato un semplice approccio matematico per la trasformazione di figure nello spazio tridimensionale in  figure piane, sia per la rappresentazione assonometrica, sia per quella in prospettiva.

 

La prima è più adatta alla rappresentazione di solidi o curve matematiche per la visualizzazione di soluzioni di problemi geometrici, la seconda per la rappresentazione di costruzioni  architettoniche.

 

Per quest’ultima, si sottolinea l’estrema facilità di individuare il punto di osservazione più adatto, variando opportunamente i  parametri relativi alla posizione dell’osservatore stesso.

Una volta impostato il programma, il cambiamento di questi parametri porta infatti immediatamente alla visualizzazione del risultato, consentendo la scelta che maggiormente soddisfa.

Questo è incomparabilmente più comodo rispetto ai classici metodi puramente geometrici, che costringono a ripartire da zero ogni volta che si volesse portare qualche cambiamento.