Capitolo 29 )            Segnali  e  disturbi

 

 

Un segnale trasmesso a distanza è soggetto a disturbi che tendono a falsare il contenuto informativo del segnale stesso.

 

Senza indagare sulle cause di disturbo (che possono essere  interne alle apparecchiature che generano, trasmettono e ricevono il segnale, oppure esterne, dovute ad interferenze elettromagnetiche sul mezzo di supporto della trasmissione), si può dire che questo si presenta come una variazione casuale del valore istantaneo.

Finchè tale variazione è piccola rispetto all’entità dei valori istantanei del segnale, l’effetto può essere trascurato, ma in caso contrario si può giungere ad una deformazione che rende irriconoscibile (e quindi inutilizzabile)  il segnale ricevuto.

 

Un importante problema delle telecomunicazioni è quindi quello di elaborare in ricezione il segnale disturbato in modo da  estrarre da questo il segnale originario, e la tecnica numerica è particolarmente adatta  a tale scopo.

 

Esaminando la distribuzione1) del disturbo, possono essere considerati due tipi: il primo è il cosiddetto  rumore bianco, che presenta una distribuzione uniforme del disturbo casuale, cioè ogni valore compreso entro limiti definiti (massimo positivo e minimo negativo) ha la stessa probabilità di verificarsi di qualsiasi altro  nella gamma.

Più realistico è però il  rumore gaussiano, che presenta una distribuzione a campana attorno al valore zero (più probabili valori piccoli rispetto a quelli grandi).

Nello studio sugli effetti dei disturbi verranno quindi utilizzati algoritmi di generazione del ‘rumore’ di entrambi i tipi.

 

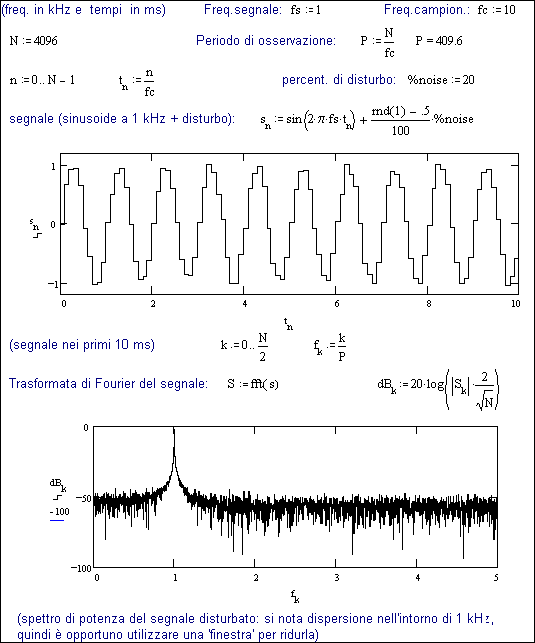
La  Fig. 29.1 esemplifica il caso di un segnale (sinusoide a 1 kHz, di ampiezza unitaria) disturbato da un ‘rumore bianco’ in percentuale variabile (%rum = 20, nell’esempio),  che viene generato con la funzione ‘random’ (rnd(1), cioè  variabile casuale fra 0 e 1), opportunamente centrata (-0.5) e divisa per 100.

Avendo scelto come numero di campionamenti N = 4096 e come frequenza di campionamento fc = 10 kHz, risulta un periodo di osservazione  P = 409,6 ms.

Nella prima parte della figura (a), viene riportato il campionamento del segnale nei primi 10 ms (dove sono visibili 10 sinusoidi, campionate ciascuna in 10 punti e dove si nota la diversità delle sinusoidi dovuta al disturbo).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fig. 29.1a  -  Generazione  ed  analisi di un segnale ad  1 kHz   con disturbo del  20%.

 

 

Il segnale vene poi trasformato in spettro (S = fft(s))  e ciascun modulo delle  k  frequenze ottenute viene rappresentato in scala logaritmica.

Si noti a questo proposito che utilizzando il coefficiente 20 come moltiplicatore del logaritmo, si esegue il quadrato del segnale 2)  quindi, per quanto visto nel capitolo precedente, si ha lo spettro della potenza.

L’osservazione riportata al fondo della fig.29.1a, consiglia l’utilizzo di una ‘finestra’ che faccia meglio risaltare i limiti delle frequenze che rappresentano il segnale, per  isolarle da tutte le altre che rappresentano il ‘disturbo’.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fig. 29.1b  -  Elaborazione del segnale precedente, per ricavarne il  rapporto  segnale/disturbo.

 

Una finestra di Hamming (v. capitolo 11) applicata al segnale, risolve il problema della dispersione spettrale, come si può osservare nella fig.29.1b qui sopra.

Quindi la potenza totale (PT) è data dalla sommatoria delle frequenze di tutto lo spettro, mentre la potenza del segnale è ricavabile dalla sommatoria delle frequenze che  ‘spiccano’ decisamente dal valore medio.

 

Il grafico sotto lo spettro rappresenta lo stesso ingrandito nella zona di  k  (da  405  a  415) ove è presente il segnale.

Si nota che la potenza è superiore a  -40 dB  per  k  tra 408 e 412, al che corrispondono frequenze  (f_k = k / P) fra  996.09   e  1005.86 Hz 3) .

 

La potenza corrispondente al segnale è dunque la sommatoria del quadrato dei moduli entro questi limiti.

Un’ulteriore precisazione sul coefficiente moltiplicatore  4/N, che è dovuto semplicemente al modo come il  MathCadâ dà il risultato della fft : in realtà ciò non sarebbe necessario perchè poi per il calcolo del rapporto segnale / disturbo si deve appunto fare un rapporto, quindi questo coefficiente si elimina 4) .

 

Il rapporto segnale / disturbo viene semplicemente ricavato dal rapporto fra la potenza del segnale (PS) e la differenza fra la potenza totale e quella del segnale (PT-PS, che è quindi la potenza attribuibile al rumore), rapporto poi espresso in dB.

 

Si osserva che la potenza totale del segnale disturbato potrebbe essere ricavata direttamente dalla sommatoria dei quadrati di s, divisa per il numero di campionamenti 5) , ma che l’analisi nel tempo non permetterebbe la distinzione fra segnale e disturbo, come fatto con lo spettro delle frequenze.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

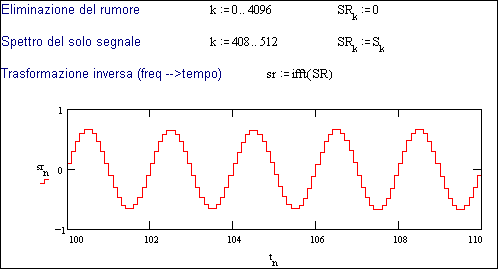
Fig. 29.1c  -  Ricostruzione del segnale con eliminazione del rumore

 

Ma l’analisi in frequenza consente di raggiungere un risultato pratico ancora  più significativo: se riusciamo a separare il segnale dal rumore, possiamo eliminare quest’ultimo e ricostruire quindi il segnale senza il disturbo. La  Fig. 29.1c mostra questa procedura sullo stesso segnale utilizzato per il calcolo del rapporto segnale/disturbo.

 

Le tecniche numeriche consentono però ancora di più: se il segnale trasmesso fosse sottocampionato, la sua ricostruzione in ricezione darebbe una serie di gradini che renderebbe evidente l’approssimazione. In questi casi si può ricorrere ad algoritmi di  interpolazione, che permettono di migliorare notevolmente il segnale in ricezione.

 

Essenzialmente il principio utilizzato è l’allargamento dello spettro (che corrisponde ad un più fitto campionamento) con la semplice aggiunta di zeri nel tratto dalla massima frequenza originale alla nuova massima.

Per tener conto di questo allargamento, occorre però moltiplicare ogni modulo originale per un coefficiente correttore.

 

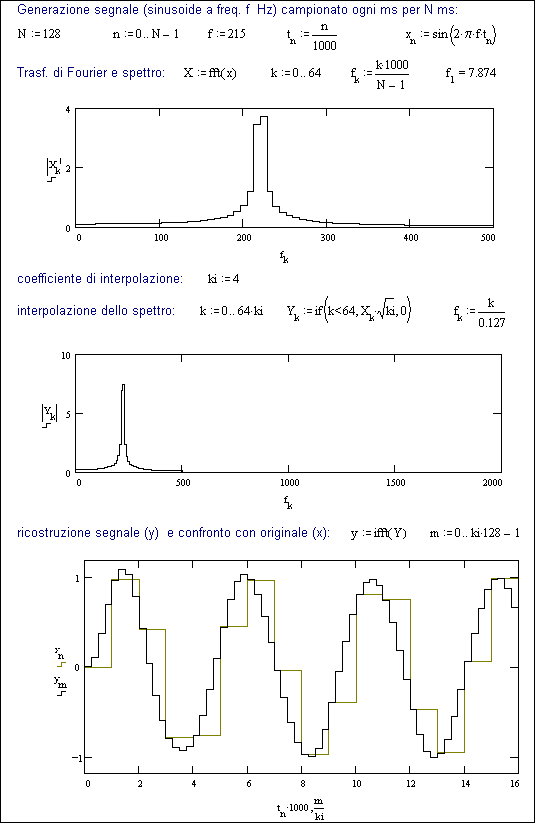
La  Fig.29.2 indica un esempio di applicazione del metodo, in cui una frequenza (f=215 Hz) è campionata ogni millisecondo (cioè meno di 5 campionamenti nel periodo).

Con un allargamento dello spettro di ki volte (ki=4 nell’esempio), si ottiene un campionamento altrettante volte più fitto, quindi una ricostruzione più accurata.

L’ultimo grafico della figura mostra appunto il confronto fra la ricostruzione con lo spettro originale (x) e quella con lo spettro allargato (y).

 

Naturalmente è possibile anche l’operazione inversa, utile per restringere la banda in trasmissione: quest’ultima è chiamata  decimazione, in quanto toglie (cioè azzera) una parte dello spettro originale.

 

Come verrà illustrato nelle appendici, queste operazioni sono facilitate dalla disponibilità di apposite funzioni software che eseguono in modo formalmente semplice tutte le procedure necessarie.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fig. 29.2  -  Esempio di interpolazione nella ricostruzione di un segnale sottocampionato.