Capitolo 28) Spettri di potenza
Un segnale fisico comporta sempre un’energia che è definita come l’integrale nel tempo della sua potenza istantanea per tutta la durata del segnale stesso.
Mentre è abbastanza chiaro questo concetto applicato ad un segnale elettrico, non altrettanto potrebbe esserlo per altri tipi di segnali quali quelli acustici oppure quelli ottici ed elettromagnetici in generale.
Per affrontare il problema è quindi opportuno iniziare l’esame di un segnale elettrico sinusoidale, per poi estenderne le conclusioni a qualsiasi tipo.
Considerando un segnale di tensione alternata sinusoidale vt = V·sen(wt) applicato ad una resistenza R, si avrà in ogni istante t una corrente it=(V/R)·sen(wt), quindi la potenza in ogni istante sarà pt = vt · it = (V2/R)·sen2(wt), che mediante identità trigonometriche[1]) può essere trasformata in
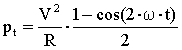
il che significa che la potenza istantanea è data da un valore costante (prodotto della ‘tensione efficace’ V/Ö2 per la ‘corrente efficace’ I/Ö2 = V/(R·Ö2) ), attorno al quale vi è un valore variabile con andamento cosinusoidale di uguale ampiezza ma di pulsazione doppia rispetto a quella del segnale.
Poiché in ogni periodo la media di questa potenza fluttuante è zero, si può concludere che il valor medio della potenza del segnale è uguale al solo prodotto dei valori efficaci, prodotto che viene definito potenza attiva.
Se ora si considera lo stesso segnale applicato non più ad una semplice resistenza ma ad un circuito composto da una resistenza R e da un condensatore C in serie, il calcolo della corrente istantanea si complica essendo questa il risultato di un’equazione differenziale.
Dovremmo infatti esprimere la tensione ai capi del condensatore come
vct = vt -
R· it con
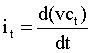
Pur essendo possibile la soluzione, ad esempio con il metodo di Laplace (vedi capitolo 7), si ritiene più intuitivo ricorrere alle differenze finite (come già visto al capitolo 16) per ottenere l’andamento di it in funzione di vt .
La Fig.28_1 mostra il caso di un circuito con resistenza R = 25 Ohm e condensatore C = 800 mFarad in serie, alimentati da una tensione sinusoidale con modulo V = 100 Volt e frequenza f = 2 Hz (quindi pulsazione w = 2pf = 4p).

Fig.28_1 - Potenza in un segnale sinusoidale.
Applicando le differenze finite si ottengono gli andamenti della tensione v e della corrente i istantanee, come indicato dal grafico.
Il loro prodotto p rappresenta la potenza istantanea ed ha un andamento sinusoidale però di frequenza doppia rispetto a v ed i, con una componente continua che rappresenta la potenza attiva.
Se infatti si fa la media di p in 1 secondo (corrispondente a N·Dt e multiplo del periodo) si ottiene il valore di questa potenza.
In elettrotecnica è però più usato il metodo vettoriale, con V ed I vettori nel piano complesso. In questo caso sono noti la tensione applicata V e l’impedenza Z (pure complessa), da cui si può ricavare I.
Indicando con a e b rispettivamente gli angoli del vettore tensione e del vettore corrente rispetto all’asse reale, può essere ricavata la loro differenza, tradizionalmente indicata come j.
La potenza attiva è allora espressa come prodotto dei valori efficaci[2]) della tensione e della corrente, moltiplicato per cos(j).
Lo stesso valore può essere ottenuto per integrazione diretta del prodotto dei segnali nel tempo.
Si noti che il valore ricavato con i vettori differisce, anche se di poco, da quello ricavato come media diretta delle differenze finite: ciò è dovuto al transitorio causato dalla costante di tempo (se ne vede chiaramente l’effetto sull’andamento iniziale del grafico della corrente e della potenza), oltre che alle approssimazioni delle differenze finite.
Questa premessa ha lo scopo di introdurre al calcolo della potenza dei segnali periodici di qualsiasi forma che, come già ampiamente citato, possono essere espressi mediante serie di Fourier, quindi come somma di segnali sinusoidali.
|
|
Fig.28_2a - Potenza in segnali con armoniche.
Il problema è dunque quello di valutare l’andamento della potenza quando coesistano nel segnale più frequenze.
La Fig.28_2a mostra il caso simile al precedente ma con l’aggiunta di una seconda armonica nel segnale di tensione, con ampiezza del 60% rispetto alla fondamentale.
La costante di tempo è stata inoltre ridotta (a 2.5 ms) per diminuire la sua influenza nel calcolo della potenza.
|
|
Fig.28_2b - Calcolo della potenza con le trasformate di Fourier.
La Fig.28_2b mostra l’applicazione delle trasformate di Fourier sui segnali di tensione e di corrente, con cui vengono ricavati il modulo e la fase di ogni vettore alle varie frequenze, per poi procedere al calcolo vettoriale della potenza.
Si noti che l’analisi è fatta su f=N/2, cioè 512 frequenze, ma in realtà nei segnali considerati sono presenti solo la fondamentale (2 Hz) e la sua seconda armonica (4 Hz), come si può constatare dal diagramma.
Il principio della sovrapposizione degli effetti, ricavare cioè la potenza come somma delle potenze calcolate per ogni singola frequenza, sembra contraddire la proprietà della convoluzione delle frequenze in corrispondenza dei prodotti dei segnali nel tempo (vedi alla fine del capitolo 6).
In realtà ciò è dovuto al fatto che l’integrale, esteso ad un periodo, del prodotto di una frequenza con frequenze sue multiple è uguale a zero, quindi la convoluzione si riduce in pratica alla somma dei prodotti dei termini di ugual frequenza.
Questo vale però solo per la parte ‘continua’ della potenza, mentre per la parte ‘fluttuante’ occorre tener conto di tutti i prodotti parziali derivanti dalla convoluzione delle frequenze di tensione per quelle di corrente.
La Fig.28.3a mostra i calcoli relativi allo stesso circuito di Fig.28.2, applicando però il metodo vettoriale. Ovviamente gli andamenti coincidono, mentre i singoli valori mostrano piccole differenze dovute al transitorio (i valori esenti dal transitorio, quindi più corretti, sono quelli di quest’ultima figura).
Dall’andamento della parte reale (attiva) della potenza, si è ricavato lo spettro che mostra la componenti continua e le armoniche a 2, 4, 6 e 8 Hz.
Nella Fig.28.3b queste componenti sono calcolate come prodotti parziali di ciascuna tensione (1° indice) per ciascuna corrente (2° indice).
Nell’esempio considerato le 2 componenti di tensione (a 2 e 4 Hz), moltiplicate per le componenti di corrente danno luogo a 4 prodotti parziali che, opportunamente raggruppati, costituiscono i coefficienti delle varie armoniche della potenza.
Per capire questo sviluppo si deve ricorrere a identità trigonometriche (come già visto all’inizio del capitolo) per cui il prodotto di due sinusoidi di uguale argomento dà una componente continua ed una di frequenza doppia.
Quindi sen2(wt)=[1-cos(2wt)]/2 e
sen2(2wt)=[1-cos(4wt)]/2
mentre sen(wt)· sen(2wt)=[ cos(wt)-cos(3wt)]/2 .
Ciò spiega [3]) l’origine di tutte le armoniche della potenza.
La Fig.28.3b riporta inoltre le espressioni relative alla potenza attiva utilizzabili per ricavare l’andamento istantaneo di questa, nelle varie possibili forme: trigonometriche, vettoriali o in serie di Fourier.
Va tuttavia sottolineato che essendo nulla la media della potenza fluttuante, il valore della potenza attiva è determinato soltanto dalla componente continua, quindi funzione unicamente dei prodotti di frequenze uguali.
In pratica lo spettro è quindi ricavato utilizzando solo queste ultime (ma ciò non permette più la ricostruzione dei valori istantanei della potenza).
Un’ulteriore osservazione è che se mancano le componenti reattive (cioè le correnti risultano ‘in fase’ con le tensioni, quindi il carico è puramente resistivo) i prodotti tensioni-correnti possono essere sostituiti da quadrati.
Infatti in tal caso P = V·I = V2/R = I2·R.
|
|
Fig.28.3b - Calcolo coefficienti dello spettro di potenza.


