Capitolo 24 )          Regolazione digitale ottimizzata

 

 

Come si è già visto precedentemente, una volta noti i parametri del sistema da controllare, cioè dopo aver ‘identificato’ il sistema, è  facile calcolare i coefficienti di un regolatore a struttura polinomiale che  dia  una risposta prefissata.

 

 

 

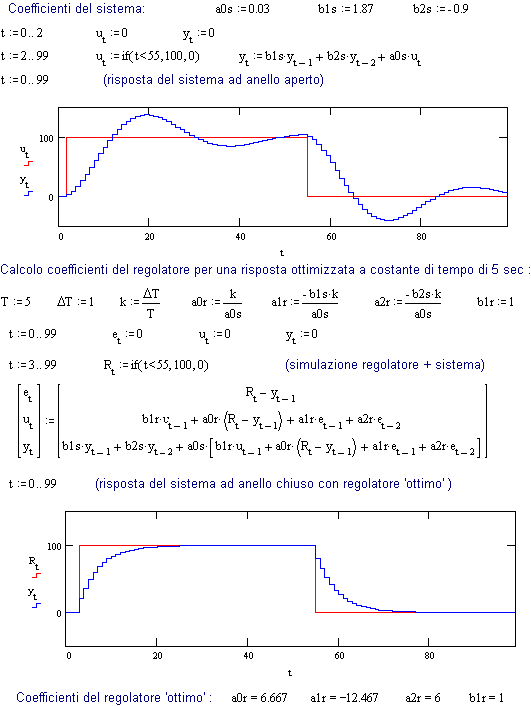
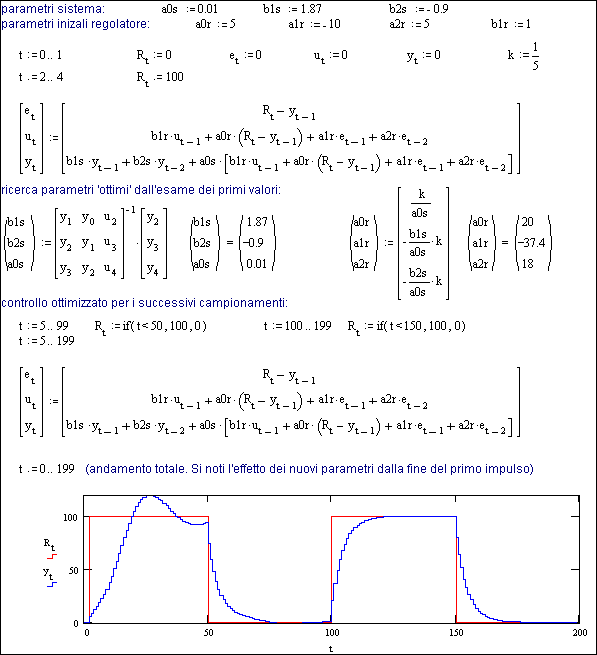
Fig. 24.1   -   Esempio di regolatore digitale ottimizzato e con risposta prefissata (T = 5 sec).

 

 

Precisamente, nota la struttura ed il valore dei singoli parametri del blocco

 

                                           a0s

                    G(z) =                                      

                                 1 - b1s·z-1 - b2s·z-2

 

(considerando il caso di un sistema con 2 costanti di tempo), si possono ricavare i coefficienti di un regolatore che faccia risultare il prodotto dei blocchi  R·G  un integratore puro come visto in  Fig. 21.4, e che quindi una volta chiuso l’anello il sistema totale corrisponda ad una costante di tempo prefissata (Tdes).

 

Si devono  pertanto calcolare i coefficienti del regolatore

 

                                a0r + a1r·z-1 + a2r·z-2

                    R(z) =                                      

                                       1 - b1r·z-1

 

                                                             DT /  Tdes

in modo che risulti       R(z)·G(z) =                              

                                                              1  -   z-1

 

La  Fig. 24.1  mostra questo calcolo partendo da coefficienti noti del sistema (ricavabili ad esempio sperimentalmente, come illustrato nel capitolo precedente), e paragonando poi la risposta ‘naturale’ del sistema (ad anello aperto, senza regolatore) a quella  ‘ottimizzata’ (col regolatore ed in anello chiuso).

 

Quello che la figura non mostra è che per ottenere queste prestazioni, l’uscita del regolatore  (u)  deve poter raggiungere in corrispondenza del gradino di riferimento,  valori molto alti (precisamente l’ampiezza del gradino moltiplicato per  a0r, quindi nell’esempio  6.667 volte il gradino stesso).

Se ciò non può avvenire e, per effetto della ‘saturazione’  del regolatore,  u  viene limitato ad un valore più basso,  non solo non si ottengono le prestazioni desiderate, ma vi è anche pericolo di instabilità.

 

Si osservi tuttavia che l’ampiezza della correzione dipende dal rapporto   DT / Tdes,  cioè dal periodo di campionamento  rispetto alla costante di tempo desiderata: se non si vuole diminuire quest’ultima occorre cercare di ridurre il primo [1]).

 

Come è già stato detto, solo con una simulazione che eventualmente tenga conto dell’effetto saturazione è possibile progettare buoni regolatori digitali ottimizzati ma, data l’importanza concettuale, verranno comunque illustrati nel seguito di questo capitolo altri metodi teorici di  autosintonia (self-tuning) e di  autoadattività  (adaptive control).

 

La differenza fra queste due forme di adattamento automatico del regolatore ai parametri del sistema, consiste  semplicemente nella invarianza di questi ultimi: se possono ritenersi costanti (almeno per un certo tempo) è sufficiente una sola taratura automatica iniziale  (‘autosintonia’), altrimenti l’adattamento deve essere continuo per seguire i cambiamenti del sistema (‘autoadattatività’).

La  prima di queste forme è ricavabile da quanto è già stato visto, unendo la procedura di identificazione con quella del calcolo dei parametri ottimi, come  nell’esempio di  Fig. 24.2.

L’assenza di disturbi di acquisizione (dovuta alla simulazione), rende applicabile il minimo numero di equazioni (3) necessarie per ricavare i parametri del regolatore ottimizzato, che sono quindi disponibili già dalla quinta scansione (sempre considerando il caso di 2 costanti di tempo). 

 

 

Fig. 24.2   -   Esempio simulato di  autosintonia.

 

 

Nell’applicazione pratica,  l’autosintonizzazione viene avviata su apposito comando ed in concomitanza con uno speciale impulso di riferimento. Naturalmente deve essere ripetuta quando si  ritenga che il  sistema controllato  abbia  cambiato le sue caratteristiche.

 

Esempi di applicazione potrebbero essere la temperatura di una cella di trattamento termico, la cui dinamica varia in funzione della massa  sottoposta a riscaldo, oppure il movimento di un carrello che varia in funzione della massa  caricata.

 

Occorre tuttavia valutare l’influenza degli errori di acquisizione e potrebbe essere necessario ricorrere a forme più sofisticate di calcolo, quale quello ai minimi quadrati visto in  Fig. 23.7, con un numero di  osservazioni superiori a quanto strettamente richiesto dal numero di  parametri da determinare.

Ciò comporta complessità (e tempi) di calcolo, con apparati allo stato attuale difficilmente  giustificabili  dal punto di vista economico.

 

Ancor  più  problematica  appare  la realizzazione  di apparati di  valutazione continua, cioè  autoadattativi.

 

L’osservazione  principale è che qualsiasi  algoritmo di identificazione del sistema controllato in presenza di disturbi, richiede che il segnale d’ingresso al sistema (u)  abbia una variazione  rispetto all’istante precedente di molto superiore al possibile disturbo.

 

In altri termini il sistema può essere identificato solo in presenza di forti variazioni  del segnale d’ingresso e una  lenta deriva dei parametri non è quindi rilevabile se non con brusche variazioni del segnale uscente dal regolatore, ma questo però contrasta con la regolarità  della stessa azione di controllo.

 

La  Fig. 24.3  rappresenta  il principio su cui si basano i sistemi autoadattativi, che va però interpretato  tenendo presente l’osservazione precedente.

 

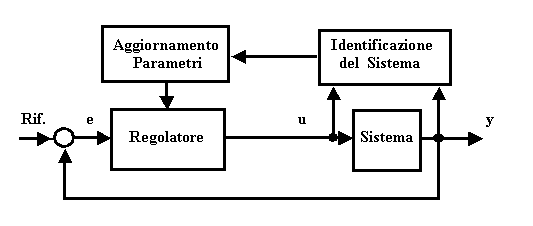
Fig. 24.3   -   Principio della regolazione autoadattativa.

 

A chiarimento del problema, è opportuno sottolineare che ciò ha ragione di essere solo se il sistema controllato ha parametri che variano nel tempo.

 

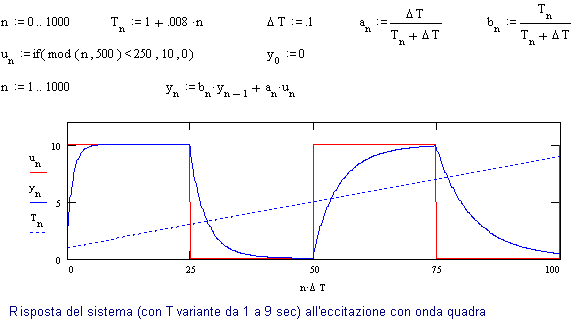
La  Fig 24.4a esemplifica un possibile sistema in cui si suppone una  sola ‘costante di tempo’  T , che ha però un andamento variabile nel tempo.

Nella versione digitale, questo dà luogo alla definizione di 2 parametri a e b  [2]), ovviamente anche loro variabili nel tempo.

 

L’andamento della risposta al gradino di tale blocco dipende quindi dall’istante in cui si applica il gradino o, meglio, dai valori di  T negli intervalli di risposta. La  figura mostra chiaramente  tale comportamento.

 

 

 

 

Fig. 24.4a  -  Esempio di sistema con ‘costante di tempo’ non fissa, ma  variabile (linearmente) nel tempo.

 

 

Il tentativo di applicare un regolatore per ottenere un certo andamento desiderato non può quindi avere successo con un normale regolatore a parametri fissi ed è quindi evidente che soltanto con un regolatore autoadattativo si possa raggiungere lo scopo.

 

La  Fig.24.4b mostra i risultati con regolatori dei due tipi, entrambi tarati per ottenere Tdes = 2 sec .

Nel secondo caso l’autoadattività è stata però ottenuta in anticipo (‘fuori linea’), supponendo la conoscenza preventiva dell’andamento di T, il che non è generalmente possibile  nelle applicazioni pratiche. Da qui l’interesse per procedure di autoadattività  in linea.

 

 

Fig.24.4b  -   Regolazioni del sistema  a  T variabile della  Fig.24.4a.

Confronto fra regolatore a parametri fissi  e  regolatore autoadattativo (cioè con parametri variabili  calcolati in  funzione della variazione di T ).

 

 

 

 

I metodi di identificazione ‘continua’ si basano su procedimenti di tipo ricorsivo cioè su una valutazione che si aggiorna ad ogni nuovo campionamento.

 

La  Fig. 24.4c mostra un esempio di regolazione autoadattativa dello stesso sistema  prima esaminato, con  T  variabile linearmente da 1 a 9 sec. 

 

Il calcolo dei parametri del sistema viene fatto ad ogni scansione, basandosi sul sistema di equazioni di pag. 23-7  per ricavare i parametri  del sistema (a0s e b1s) dai valori di  u  e   y.

 

                               ( y t-1 ) 2  -   y t-2·y t                                             y t·u t-1 -  y t-1·u t 

Risulta:     a0st  =                                               b1st  =

                                y t-1·u t-1 -  y t-2·u t                                  y t-1·u t-1 -  y t-2·u t 

 

 

Questi vengono utilizzati  per ricavare i parametri ‘ottimi’ del regolatore (a0r  e  a1r), seguendo le relazioni di pag. 22-2.

 

 

                T  +   DT                                       -T

  a0r  =                                           a1r  =                                    b1r  = 1

                  Tdes                                          Tdes

 

 

Poichè  in un sistema con semplice costante di tempo e guadagno unitario è anche:

 

                    DT                                               T

  a0s  =                                         b1s  =

               T  +   DT                                     T  +   DT

 

 

si possono esprimere i parametri del regolatore in funzione dei parametri del sistema

(eliminando T):

 

                 DT                                            - DT · b1s

a0r  =                                           b1r  =

            Tdes ·a0s                                      Tdes · a0s

 

 

 

Le espressioni nel procedimento di simulazione della  Fig. 24.4c, sono quindi il risultato della composizione del metodo di identificazione con quello di ottimizzazione, per ottenere (almeno in teoria)  una risposta prefissata  Tdes, anche nel caso di  T  variabile.

 

Il riferimento  R  è un’onda quadra fra  +10  e  - 10 e l’andamento di  y  mostra che questo viene seguito con una ‘risposta’  pressochè costante, corrispondente  a  Tdes = 2 sec.

 

 

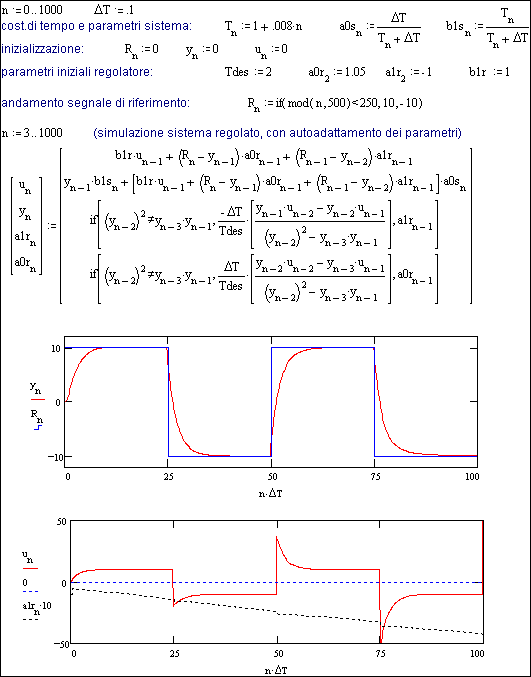
Fig. 24.4c  -  Esempio (semplificato) di procedura  autoadattativa.

 

 

 

Ovviamente ciò richiede un ‘forzamento’ sempre più spinto man mano  T cresce  rispetto   Tdes  (cioè il segnale u d’ingresso al sistema deve raggiungere valori sempre più elevati),  il che è visualizzato nei picchi dell’ultimo grafico della figura.  Questo presuppone la mancanza di qualsiasi limitazione, cioè che il regolatore non si ‘saturi’  [3]).

 

L’ultimo grafico mostra anche l’andamento (amplificato) di uno dei parametri del regolatore autoadattativo (a1r).

Per sistemi a molti parametri si deve ricorrere al calcolo matriciale e il metodo più adottato in questo caso è quello noto come  RLS (Recursive Least Square, ossia ricorsivo ai minimi quadrati) 

 

Nota la stima dei parametri riferita al campionamento precedente (rappresentata dalla matrice qt-1), si tenta di prevedere quale sarà l’attuale valore di uscita (yt  dovrebbe essere uguale a   MTt · qt-1, dove MTt  è la matrice degli stati rilevati nel campionamento attuale). In generale si avrà però una differenza dovuta sia alla variazione dei parametri sia alla presenza di errori. 

 

Si può quindi scrivere un’equazione matriciale che ricavi la nuova stima dei parametri

 

                          q t  =  q t-1 +  gt · ( yt - MTt · q t-1)

 

dove   gt   è una ‘matrice correttiva’ che permette di calcolare la variazione dei parametri dall’errore di valutazione riscontrato.

 

Questa può essere espressa in funzione di un’altra matrice  P che inizialmente è una ‘matrice identità’  I  [4])   e che tiene conto degli scostamenti quadratici dell’errore

 

Senza entrare nella dimostrazione, il metodo ricorsivo richiede ad ogni scansione l’esecuzione della seguente serie di  calcoli matriciali:

 

                         g t  =   Pt-1 · M t · ( MTt · Pt-1 · M t + 1)-1

                         q t  =  q t-1 +  gt · ( yt - MTt · q t-1)

                         Pt  =  ( I -  gt · MTt ) · Pt-1

 

Come si vede, la complessità di questi calcoli giustifica quanto è stato detto alla fine del capitolo precedente, in quanto non solo l’implementazione algebrica risulta difficile anche per pochi parametri, ma soprattutto i tempi di calcolo diventano proibitivi per applicazioni ‘in linea’.

 

 

Considerando il caso molto semplice (ma anche spesso sufficiente in pratica) di una sola costante di tempo  e di guadagno unitario, come considerato nell’esempio di  Fig. 24.4c, viene indicato in  Fig. 24.5 un metodo di identificazione elementare ma molto ‘robusto’ (cioè meno sensibile agli effetti dei disturbi), implementato in linguaggio Basic.

 

Poichè in questo caso  vale        yt = b1s· yt-1 +a0s· ut   con   b1s+a0s = 1,

indicando con  b la stima del parametro b1s, si ottiene:

 

      yt =  b·yt-1 + (1- b)·ut        da cui           b = (yt - ut ) / (yt-1 - ut )

 

If yp<> u And Abs(y - yp) > dmx  Then

     b = (y - u) / (yp - u)

     If b > bp + pmx Then b = bp + pmx

     If b < bp - pmx Then b = bp - pmx

  End If

  bp=b 

a) programma Basic (da eseguire ad ogni scansione).

 

1
 

.8
 

.6
 

b
 

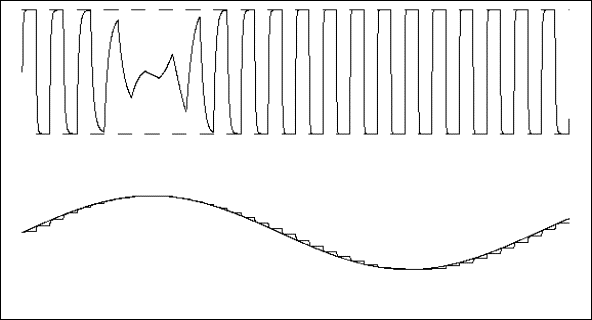
b) sistema eccitato con onda quadra senza disturbi

 

b
 

.6
 

.8
 

1
 
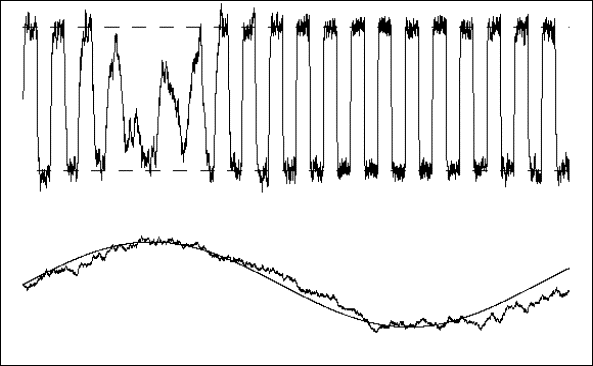
 c) sistema eccitato con onda quadra in presenza di forti disturbi

 

Fig. 24.5   -   Metodo di stima nel caso del solo parametro  b.

 

 

 

La  Fig. 24.5a  mostra l’implementazione  di questo calcolo, che deve evitare divisioni per zero ed attivarsi solo in caso di decise variazioni del segnale (superiori al massimo disturbo previsto dmx).

Per evitare la diretta influenza dei disturbi, si è posto un limite pmx alla variazioned di  b, che dovrebbe corrispondere alla massima pendenza della variazione prevista per  b1s.

 

Nella parte superiore del riquadro 24.5b viene mostrato l’andamento di  u (onda quadra) e di y (onda con andamenti esponenziali) supponendo una variazione sinusoidale del parametro  b1s  (da   0.601  a  0.999, come mostrato nella linea continua nella parte inferiore del riquadro).

La  linea a scalini è invece la sua stima, cioè  b, ricavata dal programma precedente.

 

Il riquadro 24.5c mostra la stessa situazione, ma con disturbi casuali fino al  20% del segnale: si vede che malgrado la forte distorsione, la stima di b rimane buona.

 

Un regolatore  autoadattativo ed ottimizzato, basato su questo metodo di stima avrebbe quindi come parametri:

                    DT                                  - DT · b

     a0r =                                 a1r =                                    b1r = 1 

               Tdes·(1- b)                         Tdes·(1- b)

 

La  Fig. 24.6  riporta un esempio di questo tipo, in cui all’anello viene applicato un riferimento a onda quadra  R (±10 V, a 2 Hz) e l’uscita del regolatore  u  pilota un sistema con uscita  y  e con costante di tempo T linearmente variabile da  10  a  60 ms.

 

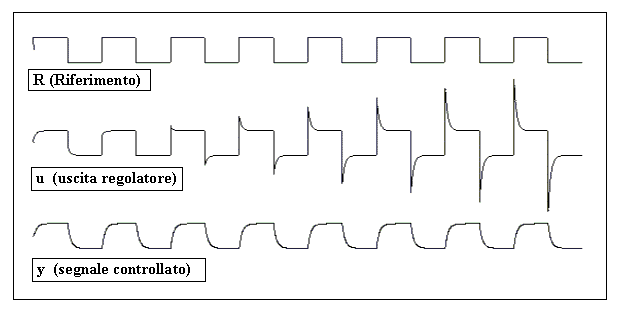
Fig. 24.6   -   Simulazione di un anello con regolatore autoadattativo su un sistema a costante di tempo variabile linearmente.

 

La costante di tempo desiderata, cioè quella che si tenta di imporre all’anello chiuso, è stata fissata in 20 msec  (Tdes = 20 ms), quindi si vede che inizialmente il regolatore deve attenuare l’uscita di controllo, mentre con il crescere di  T  deve forzarla sempre più.

 

La simulazione dimostra quindi che stimando in linea il parametro  b e calcolando con questo i parametri ottimi del regolatore, si raggiunge lo scopo di mantenere costante la risposta dell’anello pur in presenza di una notevole variazione di  T (da 1 a 6).

 

Si deve comunque ancora una volta sottolineare che tutto ciò è  purtroppo valido solo in mancanza di saturazione e che quindi tali risultati non sono  quasi mai ottenibili nelle applicazioni reali.

 

Il prossimo capitolo sarà appunto dedicato ai tentativi di minimizzare gli effetti della saturazione.

 


[1])  Per valori di  DT  diversi da 1 occorre esprimere il tempo nel programma di figura non come  t , ma come  tn = n · DT .

[2])  Vengono così indicati per brevità  i parametri  rispettivamente a0s  e   b1s  del blocco  digitale S(z) del sistema, che dipendono dalla T e dall’intervallo di scansione  DT.

Se il guadagno del blocco è unitario,  si ricorda che  a0s + b1s = 1 ( pag. 19-2).

[3])  Il caso è anche ideale perchè presuppone la mancanza di disturbi ed il fatto che  u¹0.

[4]) Viene definita matrice identità  I  una matrice costituita da valori nulli ( = 0) eccetto quelli in diagonale che sono = 1. Per una più elevata convergenza, è però opportuno che la matrice iniziale sia moltiplicata per un fattore elevato (per es. 1000).