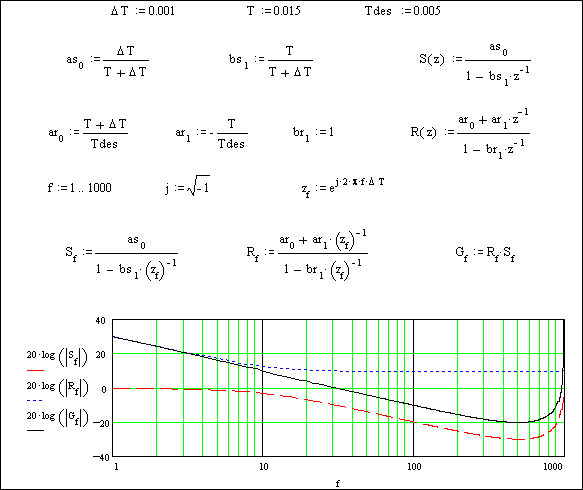Capitolo 22 ) Regolatori digitali
Un regolatore digitale è caratterizzato, oltre che dall’elaborazione numerica dell’algoritmo di controllo, anche da un ciclo di scansione, cioè da un periodo di tempo durante il quale si suppone che i segnali in gioco non varino ed entro il quale deve completarsi lo svolgimento delle operazioni di calcolo.
Più in dettaglio, una tipica configurazione di controllo digitale è rappresentabile come in Fig. 22.1, in cui gli interruttori 1 e 2 vengono chiusi in opportuna sequenza per il tempo strettamente necessario a trasferire il segnale al relativo convertitore e con un periodo di ripetizione costante, normalmente indicato con DT.
Precisamente all’inizio di ciascun ciclo viene momentaneamente chiuso l’interruttore 1 per trasferire il segnale (analogico) y al convertitore Analogico/Digitale (A/D), in modo da avere disponibile per il calcolo l’aggiornamento di questo valore, vengono poi svolti i calcoli nell’unità di elaborazione ed alla fine di questi viene momentaneamente chiuso il 2 onde permettere la conversione Digitale/Analogica (D/A) e quindi l’aggiornamento del segnale d’uscita u.
Ovviamente il segnale (analogico) u è memorizzato, cioè mantenuto costante fra un aggiornamento e l’altro, risultando quindi in realtà un segnale a gradini nel tempo, con durata di ciascun gradino uguale a DT.

Fig. 22.1 - Configurazione di una regolazione digitale.
Valgono perciò tutte le relazioni viste nei capitoli precedenti sui segnali campionati, ed in particolare è possibile convertire le funzioni di trasferimento da trasformate s di Laplace in trasformate z (vedi pag. 17-2).
Supponendo ad esempio che il sistema della Fig. 22.1 sia lo stesso visto nella Fig. 21.3 e che il regolatore sia di tipo PI, varranno le trasformazioni:
![]() S(s) = 1 / (1 + T·s) S(z) = as0 /
(1 - bs1 · z-1 )
S(s) = 1 / (1 + T·s) S(z) = as0 /
(1 - bs1 · z-1 )
![]() R(s) = (1 + T·s) / (Tdes· s) R(z) = (ar0 + ar1
· z-1 ) / (1 - br1 · z-1 )
R(s) = (1 + T·s) / (Tdes· s) R(z) = (ar0 + ar1
· z-1 ) / (1 - br1 · z-1 )
![]() G(s) = R(s) · S(s) = 1/ (Tdes · s) G(z) = a0 / (1 - b1 · z-1
)
G(s) = R(s) · S(s) = 1/ (Tdes · s) G(z) = a0 / (1 - b1 · z-1
)
dove i coefficienti del sistema sono, come già visto, as0 = DT / ( T + DT)
e bs1 = T / ( T + DT) , mentre ponendo quelli del regolatore ai valori
ar0 = ( T+ DT) / Tdes , ar1 = -T / Tdes e br1 = 1 si ottengono a0 = DT / Tdes e b1 = 1 , cioè i coefficienti di un nuovo blocco integratore puro con costante Tdes .
La Fig. 22.2 mostra in programma Mathcadâ la progettazione di un regolatore digitale applicato ad un sistema con una costante di tempo T = 15 ms (il che corrisponde ad una frequenza di taglio di circa 10 Hz) in cui si desidera raggiungere una costante di tempo dell’anello chiuso Tdes = 5 ms. Come tempo di scansione si è scelto DT = 1 ms .
I diagrammi di Bode rispettivamente del sistema S, del regolatore R e dell’intero anello (aperto) G, mostrano l’effetto di ‘compensazione‘ del regolatore per ottenere un integratore puro, cioè una retta con inclinazione di -20 dB / decade, che tagli l’asse 0 dB alla frequenza desiderata di 1/(2·p·Tdes) @ 32 Hz.
I diagrammi mostrano anche chiaramente l’effetto della scelta del tempo di scansione: aliasing oltre i 500 Hz (cioè la metà della frequenza di scansione, che con DT = 1 ms corrisponde ad 1 kHz).
|
|
Fig. 22.2 - Calcolo di un regolatore digitale con
risposta prefissata
La chiusura dell’anello su un integratore puro genera, come già visto, un blocco equivalente ad una costante di tempo , che nel caso specifico corrisponde a Tdes = 5 ms.
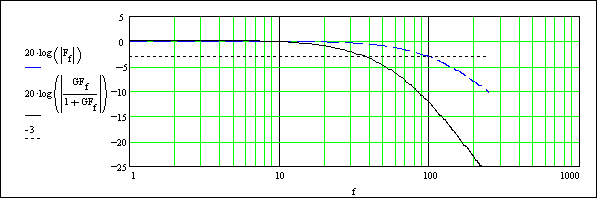
La Fig. 22.3 mostra la risposta dell’anello chiuso, considerando l’introduzione di un filtro (analogico, del secondo ordine) antialiasing sui segnali d’ingresso di riferimento e di retroazione con banda passante [1]) di 100 Hz.
L’andamento del filtro è rappresentato dalla linea a tratti, mentre la risposta dell’anello chiuso, comprendente il filtro, è rappresentata dalla linea continua.
Come si vede la banda passante dell’anello chiuso è circa 32 Hz ed assumendo in prima approssimazione che corrisponda ad un blocco con una sola costante di tempo [2]), questa risulterebbe infatti 5 ms
|
|
Fig. 22.3 - Risposta dell’anello chiuso, tenendo conto dell’inserimento di un filtro antialiasing.
Si può quindi assumere come funzione di trasferimento dell’anello chiuso la funzione
H(z) =G(z) / (1+ G(z)) = ah0 / (1 - bh1 · z-1
)
con ah0 = DT / ( Tdes + DT) e
bh1 = Tdes / ( Tdes + DT)
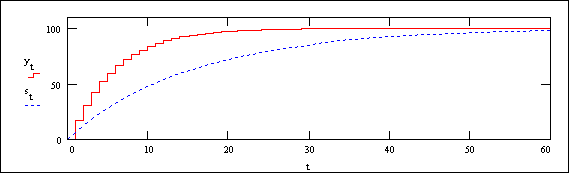
Trasformando nel tempo la H(z) si può ricavare con calcolo ricorsivo ad esempio la risposta al gradino Rif = 100 .
La Fig. 22.4 mostra questo esempio, in cui si è assunto:
y0 = 0 yt = yt-1 · bh1 + Rif · ah0 con ah0 =1 / 6 e bh1 = 5 / 6
|
|
Fig. 22.4 - Risposta al gradino dell’anello chiuso, paragonata alla risposta ‘naturale’ del sistema S (linea tratteggiata).
Come ci si aspettava, si vede che la costante di tempo è effettivamente di 5 ms
Nella figura è anche rappresentata la risposta che si sarebbe ottenuta applicando direttamente il gradino di riferimento al blocco originario, senza regolatore e senza la chiusura dell’anello, cioè utilizzando rispettiva-mente i coefficienti as0 e bs1 , anzichè ah0 e bh1
Con il metodo di progettazione illustrato è quindi possibile prefissare la risposta desiderata ed è importante sottolineare che, almeno in linea teorica, con i regolatori digitali risulterebbe possibile compensare qualsiasi struttura del sistema controllato.
Una struttura di regolatore polinomiale, permette sempre infatti il calcolo dei suoi vari coefficienti in modo tale da ‘annullare’ esattamente i poli e gli zeri del sistema controllato, comunque questo sia complesso.
Già una semplice struttura
biquadratica (vedi pag. 18-1) con 5 coefficienti è superiore in questo senso ad un classico regolatore
PID.
Ovviamente però anche per le soluzioni digitali valgono le limitazioni di carattere fisico viste per i corrispondenti regolatori analogici, eventualmente aggravate da eventuali limitazioni pratiche di calcolo (ad esempio con l’utilizzazione di numeri interi che permettono una elevata velocità di elaborazione, ma pongono limiti nei valori massimi o nel troncamento dei risultati).
Occorre quindi molta prudenza nell’applicazione pratica di metodi di ottimizzazione, che devono essere almeno supportati da simulazioni specifiche, tendenti a controllare i limiti delle grandezze in gioco.