Capitolo 21 ) Controllo in anello chiuso
Il concetto di funzione di trasferimento introdotto nel capitolo 6 consente di prevedere il comportamento di un blocco, prevedere cioè quale sarà l’andamento nel tempo del segnale d’uscita y, quando venga applicato al suo ingresso un segnale x di cui sia noto l’andamento nel tempo.
In pratica si è visto che ciò è possibile ricavando prima da x lo spettro X(f) moltiplicandolo poi per la funzione H(f) del blocco ed antitrasformandone infine il risultato.
Il problema del controllo, cioè l’imposizione di un certo andamento del segnale d’uscita da un blocco, è quindi concettualmente riconducibile all’inverso di questo schema di calcolo: prefissando y si deve stabilire quale deve essere x.
Tale metodo è noto come controllo ad anello aperto (open loop control) ed ha forti limitazioni pratiche in quanto non dà alcuna garanzia circa l’effettiva precisione ottenibile.
Come esempio molto semplice si pensi alla temperatura di un forno che può essere controllato agendo sulla portata di combustibile o sulla potenza fornita (nel caso di forno elettrico): anche determinandone accuratamente il modello di comportamento, cioè tipo e parametri della funzione di trasferimento, è abbastanza intuitivo che il controllo della sua temperatura non possa essere che grossolano, poichè il sistema è soggetto a molte cause di variabilità di cui è praticamente impossibile tener conto.
Essenzialmente il modello di comportamento di un forno potrebbe essere pensato come costituito da una capacità termica (l’attitudine ad accumulare il calore fornito al forno stesso, innalzandone la temperatura) e da una resistenza termica (parametro relativo alla dissipazione del calore nell’ambiente, che quindi tende a ridurre la temperatura raggiunta).
Una configurazione elettrica equivalente (cioè un modello elettrico del forno) è rappresentato nella Fig. 21.1, in cui i rappresenta la potenza P fornita (in Watt), C la capacità termica (in W×s/°C) ed R la resistenza termica (in °C/W). Il prodotto T = R·C (in sec) è la costante di tempo del forno che caratterizza la funzione di trasferimento (in termini s di Laplace)
![]()
dove q(s) è la temperatura del forno (in °C), cioè la variabile di uscita del blocco,
corrispondente alla tensione v del
modello elettrico.
Vale pertanto quanto visto al capitolo 7, con l’unica osservazione che il circuito di Fig. 21.1 è ‘duale’ di quello della Fig. 7.1: ciò è dovuto alla scelta della corrente i come segnale d’ingresso anzichè v.
In questo caso il segnale
d’uscita ![]() corrisponde anche
a vR = iR · R , con iC + iR = i .
corrisponde anche
a vR = iR · R , con iC + iR = i .
Supponendo che da uno stato iniziale di i = 0 e vc = vR = 0, venga fornita una i ¹ 0 di valore costante (gradino), è molto intuitivo l’andamento della tensione d’uscita: al primo istante sarà iC = i, cioè tutta la corrente disponibile tenderà a caricare il condensatore, ma appena questo si carica la sua tensione vC tenderà a scaricarsi sulla resistenza con una corrente iR = vC / R.
Quindi iR continuerà ad aumentare finchè tutta la corrente disponibile alimenterà la resistenza ( iR = i e di conseguenza iC = 0), raggiungendo l’equilibrio vC = i · R.
Analogamente a quanto visto a pag. 7-3, l’andamento dell’uscita è di tipo esponenziale
vC = i · R ·
(1 - e-t / R·C)
con un valore di pendenza iniziale uguale a i / C . Tale pendenza si riduce progressivamente pure in modo esponenziale[1]) tendendo ad azzerarsi quando t tende all’infinito, cioè si ha un andamento orizzontale al valore di equilibrio i · R.
Si osservi che se R tende all’infinito l’andamento diventa lineare, riducendosi alla sola azione integrale di C sulla costante i e, almeno in teoria, vC tende a crescere illimitatamente.
L’equivalenza con il comportamento del forno deriva dalla constatazione che applicando una potenza riscaldante P costante, l’andamento della sua temperatura q segue una curva esponenziale dello stesso tipo
q = P · R · (1 - e-t / R·C)
dove naturalmente R e C rappresentano rispettivamente la resistenza e la capacità termiche.
L’osservazione fatta sulla pendenza iniziale e sul valore finale (asintotico) consente di ricavare sperimentalmente i due parametri:
C = P / (Dq0/Dt0) (cioè la potenza divisa per la pendenza iniziale)
R = qmax / P (cioè la massima temperatura raggiunta a regime divisa per la potenza fornita)
Con un tale modello sarebbe certamente possibile prevedere e quindi controllare il valore di temperatura ad ogni istante conoscendo l’andamento di P anche variabile nel tempo ma, come già detto, la precisione pratica ottenibile sarebbe piuttosto scarsa.
Per il controllo di una grandezza fisica, quale appunto la temperatura, si preferisce ricorrere alla determinazione dell’ errore, cioè della differenza fra il valore voluto (riferimento) e valore effettivo (retroazione).
Il termine ‘Retroazione’ esprime il concetto dell’influenza del valore d’uscita sulla formazione del segnale di controllo ed in effetti la configurazione del blocco si modifica come in Fig. 21.2.

Fig. 21.2 - Principio del controllo con retroazione.
Da tale caratteristica questa configurazione prende il nome di controllo ad anello chiuso (closed loop control) e costituisce la base della regolazione automatica.
L’ utilizzazione dell’ errore come segnale di controllo consente infatti di ottenere risultati praticamente indipendenti da qualsiasi causa, quale l’influenza di segnali di disturbo o non-linearità del sistema, che tenda a modificare la variabile controllata rispetto al segnale di riferimento.

Fig. 21.3 - Anello di regolazione automatica.
Esaminando più in dettaglio le relazioni che legano le grandezze nell’anello si evidenzia però la necessità di introdurre nell’anello stesso un blocco che trasformi opportunamente l’errore.
La Fig. 21.3 mostra un tipico anello di controllo della grandezza y , in cui si evidenzia il blocco regolatore che ha come ingresso l’errore e e come uscita il segnale u.
Chiamando rispettivamente R e G le funzioni di trasferimento del blocco regolatore e del blocco sistema, si può scrivere simbolicamente
u = e · R e y = u·G quindi y = e·R·G
ma poichè e = Rif - y è y / Rif = R·G / (R·G + 1)
Questo rapporto può essere interpretato come la funzione di trasferimento globale dell’anello chiuso (blocco a tratteggio della Fig.21.3) e si vede che può considerasi uguale all’unità se il prodotto R·G è molto grande rispetto a 1. Ciò significa che in tale condizione y = Rif, cioè la grandezza d’uscita è uguale al segnale di riferimento.
Altra importante considerazione è che fissata una data funzione di trasferimento globale Gdes , può essere ricavata quella del regolatore corrispondente:
R = Gdes / [G· (1 - Gdes)]
In altre parole il comportamento desiderato dell’anello globale può essere stabilito preventivamente. Questo in linea teorica perchè, come si vedrà più avanti, le limitazioni fisiche del blocco regolatore non sempre ne permettono la realizzazione pratica.
Considerando la regolazione di tipo analogico, cioè continua nel tempo quindi non campionata, le funzioni di trasferimento devono essere espresse in termini di Laplace e supponendo che il sistema regolato sia costituito da una semplice costante di tempo (come ad esempio il forno precedentemente illustrato), si ha:
G(s) = 1 / (1 + T· s)
che si desidera trasformare in
Gdes(s) = 1 / (1 + Tdes·s)
Applicando la relazione per il calcolo di R vista poc’anzi, risulta che il regolatore deve avere una
R(s) = (1 + T·s) / (Tdes·s)
Passando ai termini di Fourier, cioè ponendo al posto di s la pulsazione jw, e rappresentando poi le varie funzioni di trasferimento nel diagramma di Bode si può interpretare graficamente il risultato ora visto.
Nella Fig. 21.4 sono rappresentati (in forma stilizzata e ridotti a semirette, date le scale logaritmiche) gli andamenti dell’ampiezza in funzione di w, di ogni funzione considerata.

Fig. 21.4 - Rappresentazione in diagramma di Bode delle funzioni di trasferimento del sistema originario (G), del regolatore (R), del loro prodotto (G·R) ed infine del blocco risultante dalla chiusura dell’anello (Gdes)
Ciò è quanto dovrebbe fare ogni buon progettista di regolatori per ricavare i parametri di R(w) una volta noto G(w) ed avendo fissato Tdes (cioè Gdes).
Si noti che affinchè Gdes sia una costante di tempo con frequenza di taglio desiderata corrispondente ad 1/Tdes, il prodotto G(w)·R(w) dei due blocchi ad anello aperto deve essere una retta (rappresentata in figura a punto e linea) con pendenza 20 dB/decade e passante per wd=1/Tdes.
Il regolatore risultante deve seguire questa retta per valori di w<1/T (comportamento integratore) e rimanere costante per valori di w>1/T (comportamento proporzionale), quindi il regolatore dovrà essere di tipo PI (sigla che indica appunto le azioni proporzionale ed integrale).
Una possibile realizzazione pratica di tale regolatore è rappresentata nella Fig. 21.5, in cui è mostrato l’impiego di un amplificatore operazionale che svolge sia la funzione di calcolo dell’errore ( e = Rif - y) mediante le resistenze d’ingresso Ri, sia la funzione PI mediante il circuito di reazione Rr·Cr. Poichè l’uscita u dell’ amplificatore operazionale è invertita rispetto al suo ingresso, in realtà viene applicato a questo il valore -e (-Rif e +y attraverso le resistenze Ri).
Si ricorda inoltre che poichè il guadagno dell’amplificatore operazionale è da ritenersi infinito, e quindi la sua corrente d’ingresso è praticamente zero, per il nodo d’ingresso vale la relazione
-Rif/ Ri + y / Ri + ir = 0 cioè e / Ri = ir
dove ir è la corrente nel circuito di reazione, in cui
u =
ir · Rr + ir / (Cr·s) (si noti l’uso dell’operatore s di Laplace per
esprimere l’integrazione di ir)
In definitiva, sostituendo ir , la funzione di trasferimento del regolatore è data da:
u / e = Rr / Ri + 1 / (Ri ·Cr ·s) = (1 + Rr·Cr ·s ) / (Ri·Cr·s)
Come si vede è la stessa R(s) di prima con T = Rr·Cr e Tdes = Ri·Cr.
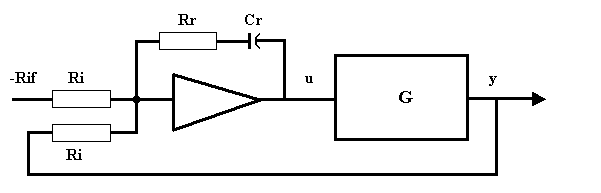
Fig. 21.5 - Esempio di regolatore analogico tipo PI con parametri compensatori di G.
Seguendo questo metodo sembrerebbe quindi risolto il problema di ottimizzazione della regolazione, nel senso che, data qualsiasi struttura di G, questa potrebbe essere ‘compensata’ da un adatto regolatore R che permetta di ottenere dall’anello chiuso una funzione di trasferimento (e perciò un comportamento) prefissata a piacere.
Purtroppo diverse considerazioni mostrano limiti alla pratica applicabilità della teoria, il che spesso demotiva i progettisti al suo utilizzo, finendo col favorire l’adozione di regolatori standard che presentano larghi margini di tarabilità, ed affidando poi la loro taratura, cioè la scelta dei parametri compensatori, a procedimenti per tentativi, che certamente non portano ai massimi risultati.
Fra le principali cause di inapplicabilità della teoria vi è soprattutto la saturazione del regolatore, cioè il raggiungimento dei margini di funzionamento reale del dispositivo.
Osservando la Fig. 21.5, si può comprendere che il segnale d’uscita u del regolatore non può andare oltre certi limiti fisici (ad esempio ±10 Volt) e che quindi al raggiungimento di questi cessa l’azione di correzione ottenuta con la chiusura dell’anello.
Del resto anche nessun sistema controllato è completamente lineare oltre certi limiti ed in tal caso cadono i presupposti su cui si basa la teoria del controllo.
Una efficace rimedio a questa situazione è il ricorso alla simulazione mediante calcolatore su modelli sia del sistema che del regolatore.
Con la simulazione è infatti possibile tener conto degli effetti della saturazione, il che permette di trovare comunque valori dei parametri che rendano massime le prestazioni ottenibili.
La Fig. 21.6 esemplifica tale simulazione applicata ai blocchi delle figure precedenti in cui sia T = 5 sec e si desideri raggiungere un Tdes = 2 sec.
Applicando le relazioni viste, si otterrebbe
R(s) = (1+5·s) / 2·s =
2.5 + 0.5 / s
cioè guadagno proporzionale Kp = 2.5 e guadagno integrale Ki = 0.5.
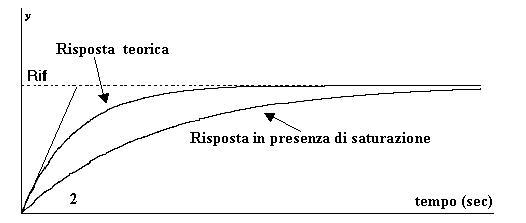
Fig. 21.6 - Influenza della saturazione sulla risposta ad un gradino.
La figura mostra però chiaramente che tenendo conto della saturazione, la risposta effettiva dell’anello si discosta notevolmente da quella prevista.
Nella pratica però spesso ci si accontenta di tarare il regolatore in modo che la risposta al gradino sia non-oscillante o con una modesta sovraelongazione (breve superamento del riferimento con rientro nella banda di tolleranza), senza prefissarne le prestazioni. Del resto quasi mai si conoscono con sufficiente precisione i parametri del sistema controllato e questo giustifica il procedimento di messa a punto per tentativi.
Va comunque sottolineato che ove si debbano garantire prestazioni, questa pratica deve essere almeno supportata da una simulazione che evidenzi i limiti del controllo e che permetta di ottimizzarne i parametri.
Ovviamente tale simulazione richiede la conoscenza del sistema controllato, e sono quindi di fondamentale importanza i procedimenti che permettono l’ identificazione del sistema stesso, procedimenti che verranno illustrati più avanti.
I regolatori analogici classici sono essenzialmente di tre tipi:
- il più semplice è il puro proporzionale (P), che permette la taratura del solo guadagno d’anello ma che presenta anche a regime, per sistemi controllati non integratori, un errore (errore statico)
- il già visto proporzionale-integrale (PI) adatto a sistemi con una sola costante di tempo e con errore statico nullo
- il più completo proporzionale-integrale-derivativo (PID) che in teoria permette la compensazione di sistemi a due costanti di tempo, ma che è di delicata applicazione per la tendenza ad esaltare i disturbi alle alte frequenze.
Nella tecnologia moderna, questi regolatori vengono sostituiti da equivalenti apparati digitali, con vantaggi di aumentata precisione, di costanza delle caratteristiche nel tempo e di semplificato interfacciamento con i calcolatori di controllo a livello superiore.
Fisicamente i regolatori digitali sono realizzati o come unità singole (single loop controller) o in apparati che svolgono in sequenza il controllo di più anelli (DDC, Direct Digital Control) con una sola unità di elaborazione.
Questi ultimi sono spesso associati ai PLC (Programmable Logic Controller) che realizzano la logica, le sequenze automatiche e gli allarmi degli impianti industriali, in modo da costituire quello che si chiama automazione industriale di primo livello, cioè il controllo automatico delle singole parti di cui è costituito un impianto industriale.
La semplicità formale nell’uso di tali regolatori, visti come una pura sostituzione dei corrispondenti analogici, nasconde spesso sia le loro maggiori intrinseche potenzialità , sia le loro limitazioni, dovute soprattutto al campionamento.
Il prossimo capitolo è appunto dedicato ad una comprensione più approfondita di questi.
