Capitolo 18 ) Strutture normalizzate

Le configurazioni per filtri ad alte prestazioni richiedono un discreto numero di coefficienti e la struttura generalizzata di Fig. 16.2 può essere estesa a qualsiasi numero di stadi di ritardo z^-1 sia nel numeratore che nel denominatore della funzione di trasferimento in z, associando a questi i relativi coefficienti di moltiplicazione a_p e b_q.

Per le applicazioni pratiche, soprattutto se queste configurazioni devono essere realizzate in hardware, è però opportuno ricorrere a forme standardizzate, con strutture minime ben definite dette forme canoniche, componibili poi in catene seriali od in blocchi paralleli per raggiungere le prestazioni volute.

Una prima forma canonica è quella biquadratica (spesso indicata nella letteratura tecnica come biquad), costituita da due stadi di ritardo nel numeratore e due stadi di ritardo nel denominatore della funzione in z :

La Fig. 18.1 mostra la struttura rappresentata in modo generalizzato (ricavata direttamente dalla Fig. 16.2) e l’equivalente forma compattata in un blocco BQ, con i relativi 5 coefficienti.

Fig 18.1 - Strutture equivalenti di un blocco biquadratico.

La procedura di progetto deve quindi stabilire prima il numero di blocchi necessari e successivamente determinare i valori dei coefficienti di ogni singolo blocco.

Con una procedura di riduzione di un polinomio di qualsiasi grado in prodotto di polinomi di secondo grado è infatti sempre possibile calcolare i valori dei relativi coefficienti sia nel numeratore che nel denominatore della funzione in z e trasformare quindi questa funzione in una equivalente serie di blocchi biquadratici.

Fig. 18.2 - Calcolo e risposta in frequenza di una configurazione biquadratica a 3 blocchi.

La Fig. 18.2 indica un esempio di trasformazione utilizzando le notevoli possibilità di calcolo offerto dal Mathcadâ.

Si suppone di avere ricavato la funzione in z con un solo coefficiente a₀ al numeratore (caso tipico dei filtri passa-basso) ed un polinomio di sesto grado al denominatore (per semplicità nell’esempio si ipotizza un binomio elevato alla sesta, che corrisponde al caso di sei blocchi in serie con la medesima costante di tempo T=10 ms, ed un intervallo di campionamento DT=2 ms).

Con il Mathcadâ (dalla versione 5+) è possibile sia ricavare il vettore v dei coefficienti sia le radici r del polinomio (nel caso specifico questo potrebbe essere evitato essendo gia note le radici esatte, ma più in generale si conosce solo il vettore dei coefficienti , quindi normalmente si devono inserire i valori in v).

Poichè è possibile che le radici risultino complesse e coniugate, occorre raggrupparle opportunamente per ricavare le 3 coppie di coefficienti b relativi a ciascun blocco biquadratico.

In pratica il programma di Fig. 18.2 consente di ricavare i coefficienti di qualsiasi struttura biquadratica a 3 blocchi, semplicemente impostando nel vettore v i corrispondenti valori dei coefficienti nel denominatore della struttura generalizzata fino ad un massimo di 6 ritardi (il primo valore si riferisce alla z^-6, e così via fino all’ultimo che deve essere 1). Ovviamente occorre impostare 0 per le eventuali potenze mancanti.

L’esempio dimostra che l’approssimazione dei calcoli porta a radici diverse fra loro,anche se di poco (in questo caso dovrebbero risultare tutte uguali).

La figura è completata dal relativo diagramma di Bode, che permette di valutare l’andamento dell’attenuazione (in dB) alle varie frequenze.

Si è volutamente prolungato il campo di osservazione a frequenze oltre quella di campionamento per dimostrare l’effetto del campionamento stesso.

Poichè l’intervallo di campionamento è DT=2 ms la frequenza di campionamento è fc=500 Hz , e il diagramma mostra un picco in corrispondenza di questa per effetto della riproduzione dello spettro, cioè per aliasing: un apposito filtro, come già illustrato nei precedenti capitoli, dovrebbe infatti essere previsto prima della conversione del segnale da analogico a digitale per eliminare qualsiasi frequenza d’ingresso superiore alla frequenza di Nyquist cioè a 250 Hz (che corrisponde al minimo nel diagramma di Bode).

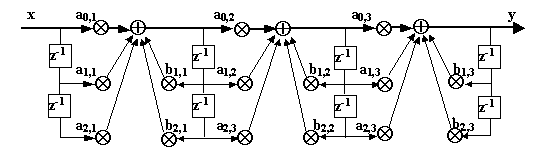
Fig. 18.3 - Configurazione tipica a 3 blocchi biquadratici.

La Fig. 18.3 rappresenta una struttura tipica composta da 3 blocchi biquadratici, i cui coefficienti sono calcolabili con il programma della figura precedente, con l’eventuale ampliamento ai coefficienti del numeratore in modo del tutto analogo.

Dopo aver visto la procedura di progetto di un tipico filtro passa-basso, si ritiene utile illustrare anche l’applicazione ad un filtro passa-banda, per evidenziare l’effetto dei coefficienti a del numeratore.

La Fig. 18.4 mostra l’effetto nel diagramma di Bode della composizione (linearizzata) di due basilari funzioni di trasferimento in s (cioè di Laplace) e precisamente il quadrato di una costante di tempo 1/(1+s·T)² , rappresentata dalla linea punteggiata, assieme ad un derivatore s·T , rappresentato dalla retta tratteggiata.

Il risultato è il prodotto delle due funzioni, che nel diagramma logaritmico di Bode corrisponde alla somma dei due grafici, e che comporta una attenuazione con pendenza di 20 dB/decade per frequenze attorno alla frequenza f_T, risultando cioè un filtro passa-banda.

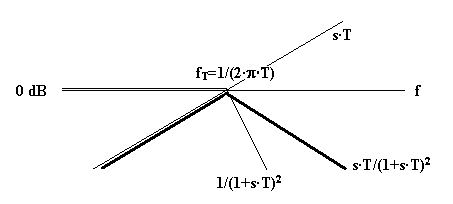
Fig. 18.4 - Composizione di funzioni di Laplace nel diagramma di Bode.

La Fig. 18.5 mostra la trasformazione di questo in z , che diventa una struttura biquadratica con i coefficienti funzioni di T e DT (solo a₂=0).

Questi coefficienti vengono ricavati con puri procedimenti algebrici, uguagliando le relative espressioni dopo aver sostituito ad s l’equivalenza in z.

Utilizzando gli stessi coefficienti per 3 blocchi ( la struttura della Fig. 18.3) e prevedendo un guadagno di 10 per compensare l’attenuazione in corrispondenza di f_T , si ottiene una H(z) come quella indicata nel diagramma di Bode della stessa figura. Per confronto, la figura è completata dallo spettro in diagramma lineare, limitato all’intorno di 10 Hz (poichè T = 15 ms risulta infatti f_T @ 10.6 Hz).

Gli esempi di calcolo dei filtri passa-basso e passa-banda ora visti possono naturalmente essere estesi anche agli altri tipi di filtri, anche a quelli ad alte prestazioni quali quelli di Butterworth, di Chebyshev, ellittici, di Bessel, ecc., ma per la progettazione pratica di questi si rimanda alle appendici.

Fig. 18.5 - Esempio di filtro ricorsivo passa-banda a 3 blocchi biquadratici.

Si deve però notare che i blocchi biquadratici possono essere messi in parallelo anzichè in serie come finora visto, applicando cioè il segnale d’ingresso x a tutti i blocchi e sommandone poi le singole uscite per formare il segnale d’uscita y.

Naturalmente i valori dei coefficienti dei vari blocchi saranno diversi da quelli calcolati per la disposizione in serie, pur conservando la struttura biquadratica.

In effetti occorre procedere alla trasformazione algebrica

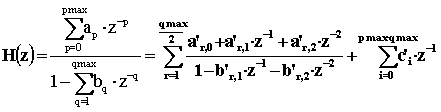
dove gli a’ ed i b’ sono espressioni algebriche dei coefficienti della forma generalizzata a e b.

I valori c’ sono coefficienti di una struttura non-ricorsiva che esiste solo se pmax>qmax.

Oltre alla struttura biquadratica esistono altre strutture standardizzate fra cui quella più promettente è la reticolare (chiamata nella letteratura tecnica lattice , letteralmente ‘a traliccio’), rappresentata nella Fig.18.6.

Il blocco di base, rappresentato nel rettangolo tratteggiato e che normalmente viene ripetuto in vari stadi, ha il vantaggio di una maggiore semplicità e di un minor numero di coefficienti, anche se il suo calcolo è più laborioso.

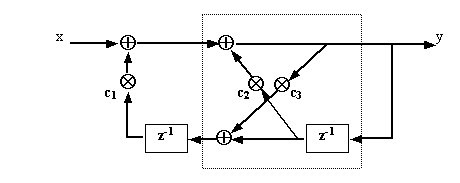
Fig. 18.6 - Struttura reticolare per la realizzazione di filtri ricorsivi.

Lo schema di calcolo nella struttura semplificata ad un solo stadio, equivale a

y_n = x_n + y_n-1·(c₁·c₃ + c₂) + y_n-2·c₁

I coefficienti c possono quindi essere ricavati da quelli della struttura generalizzata con equivalenze algebriche.