Capitolo 8 ) Limiti del campionamento

L’introduzione del concetto di spettri continui ci ha permesso di risolvere matematicamente il problema dell’ottenimento della risposta nel tempo, dato un certo segnale d’ingresso, ma solo con determinate funzioni.

Il metodo che utilizza gli spettri discreti, pur approssimato, consente invece di ottenere la risposta per qualsiasi forma del segnale, purchè periodico.

Come si è visto, l’analisi di Fourier che determina il contenuto armonico del segnale consente approssimazioni sempre più spinte più punti di campionamento vengono presi in considerazione.

In altri termini si ha maggior precisione più è piccolo il tempo fra un campionamento e il successivo, e di conseguenza più si allarga la banda delle frequenze calcolate.

A parte la limitazione pratica dell’aumento del tempo di calcolo richiesto per ottenere una certa precisione, non vi sono problemi nell’aumento delle frequenze di campionamento.

Sorgono invece problemi quando la frequenza di campionamento è troppo piccola, cioè dello stesso ordine di grandezza delle componenti armoniche del segnale considerato.

Limiti in questo senso derivano dalla considerazione che il campionamento a frequenza f_c (= 1/DT) di un’armonica di frequenza f non può essere distinta dal campionamento di armoniche con frequenze multiple f + n· f_c , dove n può essere qualsiasi numero intero, sia positivo che negativo.

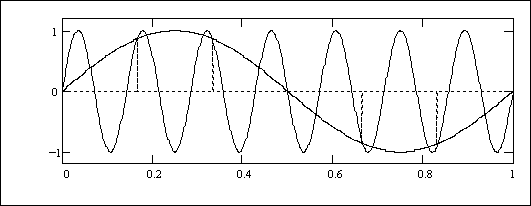
La Fig. 8.1 illustra questa asserzione, mostrando una frequenza di 1 Hz campionata a 6 Hz (quindi in 6 intervalli DT = 1/6 sec), paragonata ad una frequenza di 7 Hz sempre con il medesimo campionamento.

Fig. 8.1 - Ambiguità nel campionamento

Come si vede i campionamenti coincidono, quindi vi è un’ambiguità intrinseca nella valutazione della frequenza e si constata che gli stessi campionamenti possono rappresentare indifferentemente 1, 7, 13 .... Hz (come pure -5, -11, ecc).

Visto nella rappresentazione spettrale questo equivale a ‘repliche’ dello spettro originale, distanziate fra loro di f_c , come nella Fig. 8.2

-2f_c -f_c 0 +f_c +2f_c

f-2f_c f-f_c f f+f_c f+2f_c

Fig. 8.2 - Un’armonica f viene replicata nello spettro a multipli di f_c

Ciò può portare a gravi conseguenze perchè se lo spettro del segnale originale è più largo di f_c/2 si può avere l’introduzione nello spettro stesso di frequenze estranee, dovuta alla sovrapposizione degli spettri replicati adiacenti.

Questo fenomeno è noto come aliasing (da alias, altre, sottointendendo frequenze), ed è la base del teorema del campionamento (sampling theorem o criterio di Nyquist).

Questo stabilisce che la frequenza di campionamento deve essere almeno il doppio della frequenza della più alta armonica nello spettro del segnale, di cui non sia trascurabile l’ampiezza.

Se f_max è questa frequenza ed f_c quella di campionamento, si genera una ‘frequenza di battiamento’ f_b = f_c - f_max .

Perchè questa non entri entri nello spettro originale del segnale deve essere

f_b ³ 2 f_c , quindi f_c - f_l ³ f_max , da cui f_c ³ 2 f_max.

La Fig. 8.3 mostra casi a diverse frequenze di campionamento, supponendo di forma triangolare lo spettro del segnale convertito.

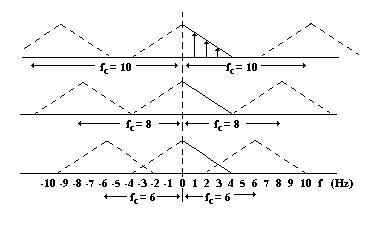
Fig. 8.3 - La replica degli spettri e possibile sovrapposizione (aliasing)

Per evitare l’effetto di aliasing si ricorre ad un filtro (detto appunto anti-aliasing) che, prima della conversione Analogico/Digitale del segnale, tagli sicuramente le frequenze dello spettro originario superiori a f_c/2 (detta frequenza di Nyquist).

In tal modo la sovrapposizione non influisce sull’ampiezza delle armoniche rimanenti.

Fig. 8.4 - Effetti della frequenza di campionamento sullo spettro del segnale

Un esempio più concreto è dato dalla Fig. 8.4, che mostra il caso di un segnale ad andamento triangolare, di frequenza 1 Hz, convertito a varie frequenze di campionamento.

In ciascuno dei casi esaminati si ha una serie di valori y_n (con n = 1...N, dove N è il numero di campionamenti nel periodo [1]⁾ ) che vengono utilizzati nell’analisi di Fourier per ricavare i coefficienti visti nel capitolo 3:

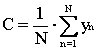
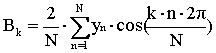
dove k è il numero dell’armonica presa in considerazione e nel caso della Fig. 8.1 varia da 1 a 20.

Dal primo spettro, con N corrispondente a 40, è evidente che le armoniche significative sono le prime quattro e che la ricostruzione con le prime 16 armoniche darebbe un risultato quasi perfetto (la Fig. 3.3 rappresenta questa ricostruzione).

Per comodità si ricorda che la ricostruzione del segnale nel tempo dati i coefficienti di K armoniche (vedi capitolo 3) è:

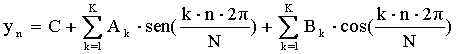
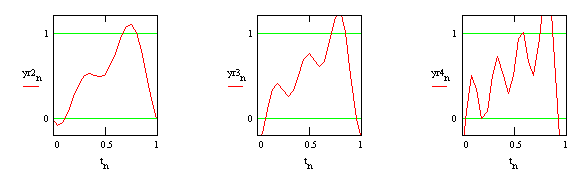
Nel secondo caso, con N = 20 e indicato con yr2 nella Fig. 8.5, si incomincia a vedere l’effetto di aliasing che, interessando solo le armoniche oltre la sesta (quindi quelle di minore ampiezza), non influiscono significativamente sulla ricostruzione del segnale.

Il terzo caso (yr3), con N = 10, mostra una distorsione anche nella terza e quarta armonica, distorsione ancor più evidente nell’ultimo caso (yr4) con N = 5.

Applicando il criterio di Nyquist prima illustrato, se nel caso considerato sono significative le prime quattro armoniche, dovrebbe essere utilizzata come minima frequenza di campionamento il doppio della quarta armonica, cioè 8 Hz (DT=0.125 sec).

La Fig. 8.5 mostra quindi l’effetto di distorsione del segnale ricostruito, dovuto all’aliasing, cioè alla sovrapposizione dello spettro ‘replicato’ sullo spettro originale,

Si noti che il numero di punti N del segnale yr_n ricostruito può essere diverso da quello del segnale originario y_n , e nella Fig. 8.5 è N = 20 (sempre con n=1...N).

Fig. 8.5 - Effetto di distorsione per aliasing nelle ricostruzione del segnale

Nei tre casi di ricostruzione della Fig. 8.5 varia soltanto il parametro K, cioè il numero di armoniche effettivamente considerato nella ricostruzione.

Con K = 2 si prendono in considerazione solo la prima e la seconda armonica, il che è il massimo permesso dal criterio di Nyquist essendo la frequenza di campionamento di 5 Hz.

Per evitare che anche queste siano distorte occorre però porre un filtro anti-aliasing che elimini, prima della conversione in valori digitali, tutte le frequenze superiori ai 2 Hz

I casi di K = 3 e K = 4 mostrano cosa accadrebbe se non si tenesse conto del criterio di Nyquist.

A conclusione di questo esempio si può dunque dire che la forma d’onda triangolare considerata può essere convertita con una buona approssimazione da una frequenza di campionamento minima di 10 Hz (8 Hz è il minimo teorico), purchè si provveda un filtro anti-aliasing che tagli le frequenze del segnale d’ingresso superiori a 4 Hz.

In generale però si deve concludere che non vi è una regola fissa per determinare ‘a priori’ la frequenza minima di campionamento, se non si conosce già il contenuto armonico (ovviamente ottenuto con una frequenza di campionamento sicuramente alta rispetto a quella del segnale).

Inoltre gli effetti di aliasing non sono le uniche cause d’errore nella conversione di un segnale reale, cioè fisicamente rappresentato da un andamento continuo (analogico) nel tempo e non da una funzione matematicamente nota, come visto finora.

---

[1]⁾ In questo esempio, dato che il periodo è 1 sec, il numero di campionamenti N coincide con la frequenza di campionamento.