Capitolo 6 ) Funzioni di trasferimento
Qualsiasi apparato che trasformi un segnale del tempo x(t) in un altro segnale y(t) sempre funzione del tempo ma generalmente di altra forma, può essere espresso con una funzione che lega, istante per istante, il valore d’uscita a quello di ingresso.
Chiamando H [1]) questa funzione, si può cioè scrivere
y(t) = H [ x(t) ]
Se la funzione fosse di tipo algebrico non ci sarebbe alcuna difficoltà a ricavare la y(t) dato qualsiasi andamento di x(t), ma quando questa funzione è di tipo differenziale, cioè comporta derivate o integrali (come la maggior parte degli apparati reali) non è affatto agevole, salvo casi particolari, esprimere matematicamente tale legame.
Fra questi casi particolari vi sono i segnali sinusoidali. Poichè infatti la derivata e l’integrale di una sinusoide è ancora una sinusoide, se pure con differenti fasi, si può più facilmente ricavare H.
Se infatti si riesce ad esprimere H come funzione delle frequenza, è possibile conoscere quale sarà il segnale d’uscita per ciascuna frequenza in ingresso.
In generale [S1][2]) un segnale x(t) sinusoidale viene trasformato in un segnale y(t) sempre sinusoidale ma con ampiezza e fase diverse.
Questo è un importante risultato, poichè ricavando con la trasformazione diretta di Fourier il contenuto armonico X(f) di un segnale d’ingresso x(t) qualsiasi (purchè periodico), si può prevedere quale sarà il contenuto armonico Y(f) del segnale y(t) in uscita.
In altri termini, lo spettro Y(f) è ricavabile dallo spettro X(f) moltiplicato per la funzione di trasferimento H(f).
Conoscendo il contenuto armonico Y(f) è infine possibile ricostruire, con la trasformazione inversa di Fourier, il segnale y(t) nel tempo.
La Fig. 6.1 sintetizza questo metodo di utilizzazione delle trasformate di Fourier.
La funzione di trasferimento[3])
H(f)
è anche nota come risposta in frequenza del blocco.

Fig. 6.1 - Schematizzazione dell’utilizzo delle trasformate
di Fourier nella determinazione del segnale d’uscita y(t) dati il segnale
x(t) e la funzione di trasferimento
H(f) del sistema.
Per esemplificarne l’applicazione si può ricorrere al caso citato nel primo capitolo (Fig. 1.2 e 1.3), in cui il segnale d’ingresso ha uno spettro X(f) composto dalla fondamentale (a 50 Hz e di ampiezza =1) e dalla, terza armonica (a 150 Hz e di ampiezza = 0.6).
Assumendo che il blocco al cui ingresso è applicato questo segnale sia un filtro passa basso ideale a 100 Hz, la funzione di trasferimento è, per definizione, uguale ad 1 per le frequenze comprese fra 0 e 100 Hz ed uguale a 0 per tutte le frequenze >100 Hz.
Il prodotto X(f) = H(f) · X(f) dà in questo caso come risultato uno spettro composto dalla sola fondamentale, mentre la terza armonica viene eliminata.
La Fig. 6.2 illustra graficamente il procedimento.
Se il blocco fosse invece un filtro ideale del tipo passa alto a 100 Hz ( H(f) = 0 per f < 100 Hz e H(f) = 1 per f ³ 100 Hz) lo spettro risulterebbe composto dalla sola terza armonica e sarebbe la fondamentale ad essere eliminata.

Fig. 6.2 - Esempio di applicazione del metodo che utilizza le trasformate di Fourier e la funzione di trasferimento per ricavare l’andamento nel tempo del segnale d’uscita dato l’andamento nel tempo del segnale d’ingresso. [commento audio]
Il procedimento ora visto consente di ricavare anche altri importanti risultati.
Se il segnale d’ingresso x(t) è costituito da un impulso di area
unitaria e di ampiezza infinita (la
funzione d definita alla fine del capitolo
precedente), si ottiene che il
prodotto Y(f) = H(f) · X(f) si riduce a Y(f)
= H(f) in quanto lo spettro
X(f) = 1.
Possiamo quindi dare un
significato fisico alla funzione di trasferimento (o risposta in frequenza) di
un blocco, essendo questa corrispondente allo spettro del segnale d’uscita dal
blocco stesso quando all’ingresso viene applicato il segnale d.
Altra importante osservazione è che matematicamente il prodotto di due spettri equivale nel tempo ad una speciale operazione chiamata prodotto di convoluzione ( qui indicata con il simbolo Ä ), che corrisponde all’integrale nel tempo del prodotto delle trasformate inverse di Fourier dei due spettri.
Chiamati A(f) e B(f) i due spettri e C(f) il loro prodotto, con a(t) , b(t) e c(t) le relative trasformate nel tempo, valgono infatti le relazioni
C(f)
= A(f) · B(f)
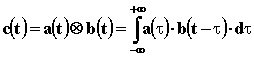
Tale operazione permette quindi di risolvere direttamente nel tempo l’equivalente di un prodotto nel dominio delle frequenze.
Vale anche l’inverso, cioè il prodotto di due segnali nel tempo comporta la convoluzione nelle frequenze
c(t) = a(t) · b(t)

Se ne vedranno le applicazioni più avanti, tentando anche di dare un significato fisico a questa operazione.