Capitolo 4 ) Spettri di frequenza
Il calcolo della serie di Fourier permette come visto in precedenza, di trasformare una tabella di dati, che rappresentano l’informazione del segnale campionato nel tempo, in una diversa tabella di dati che rappresentano il contenuto armonico del segnale.
Quest’ultima
tabella è rappresentabile in forme grafiche che prendono il nome di spettri
di frequenza.
Data la possibilità di esprimere in modi diversi l’informazione sul contenuto armonico, nella letteratura tecnica non vi è purtroppo una rappresentazione uniforme e universalmente accettata di tali grafici, per cui può esserne difficile l’interpretazione.
Si possono comunque ridurre a tre i principali tipi di rappresentazione degli spettri di frequenza relativi ad un segnale periodico.
- spettro
delle componenti immaginarie e spettro delle componenti reali.
In questo caso nel primo grafico vengono riportate sull’asse orizzontale la frequenza delle armoniche considerate (posto a 1 la fondamentale) e sull’asse verticale i coefficienti Ak , cioè l’ampiezza dei seni delle singole armoniche.
Poichè nella rappresentazione complessa queste costituiscono la parte immaginaria, questo spettro è indicato come immaginario.
Un secondo grafico dello stesso tipo riporta invece la parte reale, cioè i coefficienti Bk del coseno, più il coefficiente C per k=0.
- spettro
del modulo relativo a ciascuna armonica e spettro delle fasi iniziali.
Il modulo del vettore corrispondente a ciascuna armonica è
![]()
mentre
l’angolo di fase è dato da qk
= atan (Bk / Ak ).
- spettro
componenti vettoriali ruotanti in senso
opposto e spettro delle fasi.
Come già accennato alla fine del capitolo 2, ogni armonica può essere vista come la proiezione della somma di due vettori ruotanti sincronicamente in senso opposto, ognuno di ampiezza Mk/2.. In questo caso il diagramma completo dovrebbe comprendere anche la parte delle armoniche negative (nel senso di frequenze derivanti dalla rotazione oraria del vettore), ma questa può essere omessa essendo ovviamente simmetrica alla parte positiva, rispetto alla frequenza ‘zero’.
La Fig. 4.1 riporta gli spettri di frequenza del primo tipo, relativi ai segnali delle Fig. 3.3 e 3.4, mentre la Fig. 4.2 riporta gli spettri degli stessi segnali con rappresentazione del secondo tipo. Quest’ultima vale anche per il terzo tipo, con opportuno cambiamento di scala.
|
|
Fig. 4.1
- Esempi di corrispondenza fra
rappresentazioni di segnali nel tempo e con spettri di frequenza immaginario e
reale.
|
|
Fig. 4.2 - Esempi
di corrispondenza fra rappresentazioni di segnali nel tempo e con spettri di frequenza a modulo e
fase.
Dal punto di vista strettamente matematico, la trasformazione di Fourier di una forma d’onda y(t) di periodo P in una serie di armoniche può essere vista come la soluzione dell’equazione:
+¥
n=
1
y(t) = m 0 + S (m n · e
j n w t
+ m -n · e -j n w t)
dove w = 2·p / P , quindi una costante che rappresenta la pulsazione (rad/sec) dell’armonica fondamentale, e mn è il modulo di un vettore nel piano complesso ruotante alla velocità n·w, mentre m-n è il vettore coniugato ruotante alla velocità -n·w , cioè in senso opposto.
Per la simmetria dei due vettori, l’espressione precedente può essere anche scritta:
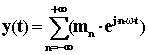
Il problema consiste quindi nel ricavare la serie mn ( con n compreso fra -¥ e +¥) che soddisfa questa uguaglianza.
L’artificio matematico che consente la soluzione è di moltiplicare entrambi i membri per e- j·k· w·t e di integrarli nel tempo per il periodo P.
Per motivi di simmetria si pone anche lo zero dei tempi a metà periodo, quindi l’integrale risulta fra -P/2 e +P/2.
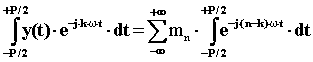
Si osserva che l’integrale al secondo membro è uguale a P per n = k e uguale a zero per n ¹ k (le aree di sinusoidi e cosinusoidi delle armoniche n·w sono nulle nel periodo P), quindi per ogni n vale:

Questa forma, anche se di scarsa utilità pratica per la difficoltà di risolvere l’integrale per qualsiasi forma d’onda y(t), ha una grande importanza concettuale in quanto consente di generalizzare la soluzione anche per segnali non periodici.
Si può infatti osservare che se P tende all’infinito, w tende a zero e le linee che rappresentano le ampiezze del modulo alle frequenze n·w si addensano sino a diventare una superficie continua.
Così n perde di significato ed è possibile sostituire n·w con w nell’equazione iniziale:
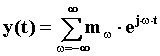
e 1/P con Dw/ 2p nell’equazione dei moduli:
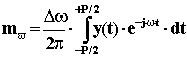
Per sostituzione si ottiene:
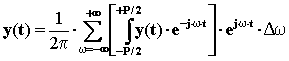
Ma se P tende all’infinito, allora Dw diventa dw e la sommatoria diventa un integrale:

L’integrale fra parentesi quadra
è lo spettro continuo di frequenza ed è generalmente indicato con G(jw).
In definitiva ciò rende possibile la trasformazione di un segnale dal dominio del tempo al dominio delle frequenze (trasformazione diretta) con:
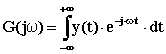
e viceversa dal dominio delle frequenze al dominio del tempo (trasformazione inversa) con:
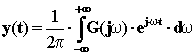
Quest’ultima forma è anche nota come integrale di Fourier.
Ricordando che w=2pf, le trasformazioni
si possono anche esprimere in funzione di
f.
Nel seguito verranno usate indifferentemente le due forme.

