Capitolo 3
) Analisi
di Fourier
Qualsiasi segnale periodico (cioè che si ripete identicamente nel tempo ad ogni periodo P ), è scomponibile in una serie di sinusoidi e cosinusoidi di frequenze multiple di 1/P.
Per illustrare il procedimento di scomposizione, si consideri il caso di una forma d’onda definita in N=8 punti equidistanti nel suo periodo.
Ponendo tale periodo P=2p [1]) l’intervallo di campionamento risulta DT=P/N = p/4.
Supponendo
che la forma d’onda considerata (vedi Fig. 3.1) possa essere espressa come somma di
2 sinusoidi (una di
ampiezza A1 e di
periodo 2p [2])
, l’altra di ampiezza A2 e di periodo p),
di 2 cosinusoidi (una di ampiezza B1 e di periodo 2p, l’altra di ampiezza B2 e di periodo p), ed infine di una componente continua C,
si può scrivere il seguente sistema di equazioni (dove yn è il valore del segnale al tempo n· DT e l’argomento delle
sinusoidi e cosinusoidi è w·n· DT) :
y1 = A1·sen(p/4) + A2sen(2·p/4) + B1cos(p/4) + B2cos(2·p/4) + C
y2 = A1·sen(2·p/4) + A2sen(2·2·p/4) + B1cos(2·p/4) + B2cos(2·2·p/4) + C
y3 = A1·sen(3·p/4) + A2sen(3·2·p/4) + B1cos(3·p/4) + B2cos(3·2·p/4) + C
............
............
y8 = A1·sen(8·p/4) + A2sen(8·2·p/4) + B1cos(8·p/4) + B2cos(8·2·p/4) + C
Si hanno quindi 8 equazioni e 5 incognite, cioè i coefficienti A1 A2 B1 B2 e C che definiscono le ampiezze delle singole armoniche.
Per risolvere tale sistema si osserva che la somma dei valori di seno e coseno per ciascuna colonna dà valore zero ( la media di una sinusoide o di una cosinusoide sul periodo o suoi multipli è infatti sempre zero).
Risulta quindi che la somma degli yn è uguale a 8 volte C, ed in generale se N è il numero di campionamenti nel periodo si avrà :
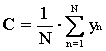
Per ricavare gli altri coefficienti si ricorre all’artificio di moltiplicare ogni riga per il termine moltiplicatore del coefficiente.
Ad esempio per ricavare A1 si moltiplicano i termini della prima equazione per sen(p/4), quelli della seconda per sen(2p/4), e così via.
Sommando ancora per colonne si ottiene che tutte le colonne , eccetto quella delle y e quella degli A1 , risultano uguali a zero.
Nella colonna degli A1 la somma dei sen2 dà come risultato 4, ed in generale N/2. Quindi :
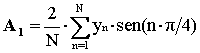
Similmente

Lo stesso vale per i coseni, cioè per i coefficienti B, ed in generale si avrà quindi:

e
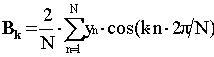
Il calcolo di questi coefficienti è noto nella letteratura tecnica come DFT (Discrete Fourier Transform) e costituisce appunto l’analisi delle forme d’onda periodiche campionate in N punti, detta anche analisi di Fourier.
In questa analisi
si evidenziano alcune caratteristiche: innanzitutto il numero di campionamenti N deve
essere pari ed
il massimo numero di armoniche considerate (qui rappresentate
con k ) è K =
N/2 - 1.
Si osserva poi che la componente continua della forma d’onda , cioè il coefficiente C, è uguale a zero se esiste una simmetria fra la parte positiva e quella negativa della forma d’onda stessa ed inoltre che i coefficienti B dei coseni sono nulli se esiste un’antisimmetria (cioè una simmetria con segno opposto) fra parte destra e parte sinistra della forma d’onda rispetto alla mezzeria verticale, cioè alla metà del periodo.
Per questi motivi l’esempio dato in Fig. 1.3 risulta composto da sole sinusoidi.
Se invece la forma d’onda presenta una simmetria speculare, sempre rispetto alla mezzeria verticale, risultano nulli i coefficienti A dei seni.
L’esempio in Fig. 3.1 rappresenta una forma d’onda composta da una costante (C), da due sinusoidi (fondamentale e seconda armonica di ampiezza rispettivamente A1 e A2) e da due cosinusoidi (di ampiezza rispettivamente B1 e B2).

Fig. 3.1
- Esempio di scomposizione di
una forma d’onda periodica in somma di
sinusoidi e cosinusoidi.
Nella figura sono
anche rappresentati gli andamenti delle singole componenti in funzione del
tempo.
Una rappresentazione vettoriale di questa forma d’onda è data dalla Fig. 3.2.
Il segnale al tempo t = 0 è la proiezione verticale della somma dei vettori (quindi C + B1 + B2). Il vettore C è costante, mentre i vettori A1 e B1 (e quindi la loro risultante) ruotano in senso antiorario alla velocità w, formando angoli wt rispetto alla condizione iniziale in figura. Così i vettori A2 e B2 e la loro risultante ruotano, sempre in senso antiorario, alla velocità 2w.
In definitiva, il segnale al tempo t è sempre la proiezione verticale delle risultanti dalla somma dei vettori ruotanti a velocità multiple di w.
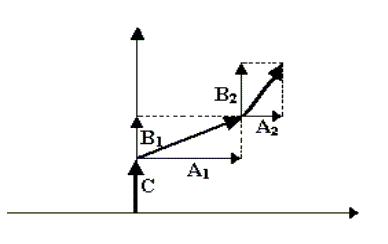
Fig.
3.2 - Interpretazione
vettoriale del segnale di Fig.
3.1 al tempo t = 0.
Chiarito il significato dei coefficienti, appare evidente che aumentando il numero delle armoniche considerate (quindi il numero dei coefficienti, cioè K), migliora sempre più la possibilità di ricostruzione del segnale originario.
Questo è infatti il risultato delle sommatorie dei coefficienti per le rispettive funzioni di seno e coseno alle varie armoniche, cioè:
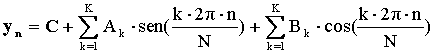
Bisogna tuttavia aver presente che K a sua volta è limitato dal numero di campionamenti effettuati sul segnale (problema questo che verrà esaminato in dettaglio più avanti), quindi vi è da rimarcare che per un segnale qualsiasi (non somma di sole alcune armoniche considerate, come si è visto finora) la possibilità di ricostruzione del segnale originario è sempre approssimata.
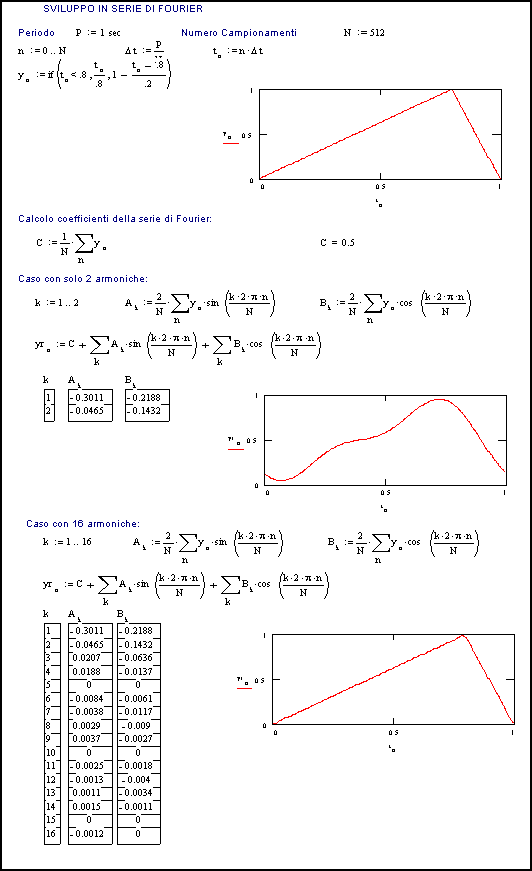
Come esempio di analisi e ricostruzione di un segnale periodico qualsiasi, si può considerare il caso illustrato nella Fig. 3.3 , elaborato in Mathcadâ.
Si tratta di un
segnale triangolare, con periodo di 1
sec, calcolato dal programma in N=256 punti, quindi un valore di yn definito in ogni istante tn.
Il programma calcola poi i coefficienti della serie di Fourier, in particolare la componente continua C , ed i valori di Ak e Bk , cioè le ampiezze delle K armoniche considerate.
Come si vede nella figura, sono stati presi in esame due casi di ricostruzione del segnale, il primo con solo due armoniche, il secondo con 16 armoniche.
Ovviamente è visibile la differenza di approssimazione nei due casi.
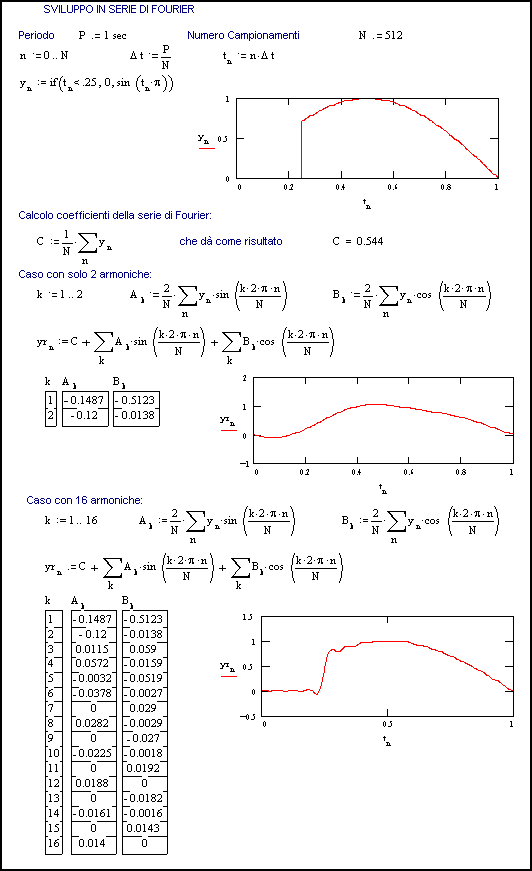
Un ulteriore esempio è dato in Fig. 3.4, dove viene esaminato una semionda di sinusoide parzializzata (tipico caso di un raddrizzatore a diodi controllati).
|
|
Fig.3.3 Esempio di analisi e ricostruzione di una forma d’onda periodica (programma in Mathcad con [commento audio])
|
|
Fig.
3.4 - Programma come nella figura precedente, ma con un segnale a semionda parzializzata