Capitolo 2 ) Sinusoidi e vettori rotanti

Una oscillazione armonica sinusoidale può essere vista come la proiezione di un vettore di modulo A ruotante nel piano, a velocità angolare costante w [1]⁾ (vedi Fig. 2.1).

Partendo dal tempo zero con il vettore orizzontale, ad ogni istante t il vettore avrà percorso un angolo wt e la sua proiezione sull’asse verticale sarà quindi una sinusoide di ampiezza A, cioè la funzione A·sen(wt).

Se la posizione iniziale del vettore forma un angolo j con l’asse orizzontale, si ha ancora lo stesso andamento della proiezione, ma la sinusoide risulterà spostata di un tempo j/w , cioè risulterà la funzione A·sen(wt+j).

Uno spostamento iniziale di 90° , in radianti p/2 e cioè vettore in posizione verticale, forma una cosinusoide, infatti :

A·sen(wt+p/2) = A·cos(wt)

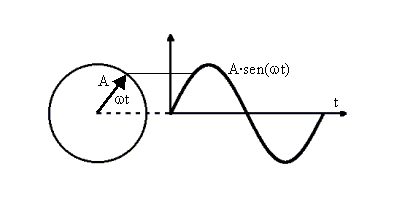
Fig. 2.1 - Sinusoide come proiezione di un vettore ruotante a velocità angolare w.

Qualsiasi posizione intermedia può allora essere vista come una composizione di una sinusoide di determinata ampiezza e di una cosinusoide generalmente di altra ampiezza :

A·sen(wt+j) = A·cos(j)·sen(wt) + A·sen(j)·cos(wt)

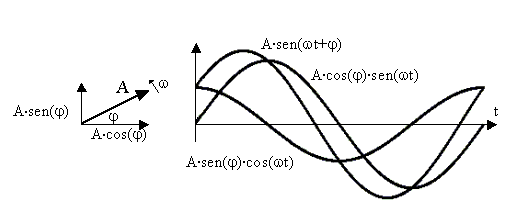
Fig. 2.2 - La proiezione del vettore A, con fase iniziale j, come somma di una sinusoide di ampiezza A·cos(j) e di una cosinusoide di ampiezza A·sen(j).

Qualunque andamento sinusoidale è quindi rappresentabile mediante le componenti orizzontale e verticale del suo vettore iniziale di fase j, e mediante la velocità angolare w di questo.

Per comodità di notazione matematica si può poi considerare tale vettore rappresentato nel piano complesso con l’asse orizzontale reale e l’asse verticale immaginario, quindi far coincidere l’ampiezza della componente cosinusoidale con l’asse reale e quella sinusoidale con l’asse immaginario.

In tal modo, ricorrendo all’uguaglianza nota come ‘ formula di Eulero ’ [2]⁾ , si può anche rappresentare il vettore A con fase j , nella forma esponenziale complessa :

A·cos( j) + j·A·sen(j ) = A·e ^{j j}

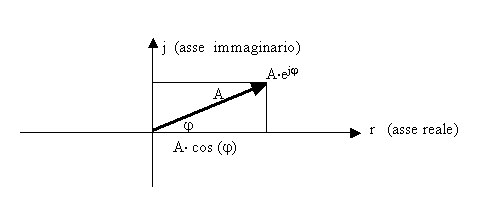
Fig. 2.3 - Rappresentazione di un vettore nel piano complesso.

Poiché il vettore ruota a velocità angolare w, ad ogni istante t si avrà:

A·e^jj·(cos( wt) + j·sen(wt)) = A·e^jj·e^jwt = A·e^j·(wt+j)

La rappresentazione in forma esponenziale complessa facilita in qualche caso l’elaborazione matematica, come si vedrà più avanti.

Un’ulteriore forma di rappresentazione definisce l’oscillazione armonica di modulo A come risultante di due vettori complessi coniugati [3]⁾ di modulo A/2 che ruotano alla velocità angolare w, ma in senso contrario uno all’altro.

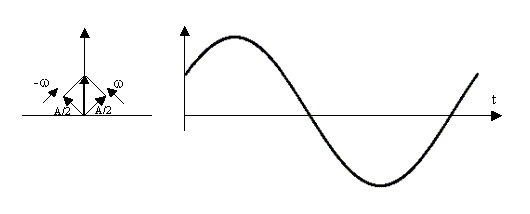
Fig. 2.4 - Rappresentazione di un’oscillazione armonica come risultante di due vettori ruotanti in senso opposto.

In tal caso si chiama frequenza negativa la rotazione in senso orario del secondo vettore (nome che evidentemente non ha alcun significato fisico), e si ha perciò una simmetria di frequenze positive e negative rispetto alla frequenza zero.

Si noti che nella Fig. 2.4 l’asse reale è quella verticale e che, data la simmetria, le componenti orizzontali (immaginarie) si annullano reciprocamente, dando luogo quindi sempre ad un risultato reale.

Si può cioè scrivere:

A·cos(w·t+j) = (A/2)·e^j·(w·t+j) + (A/2)·e^-j·(w·t+j)

Se ne vedrà più avanti l’utilizzazione nei cosiddetti spettri di frequenza.

---

[1]) w è espresso in radianti al secondo, e poiché ogni giro corrisponde a 2p rad, la velocità angolare espressa in giri al secondo (frequenza) è data da f = w / 2p.

Il reciproco di questo valore è il periodo della sinusoide, cioè il tempo dopo il quale la sinusoide si ripete identicamente.

[2]) La formula di Eulero, ricavata dai legami fra le funzioni trigonometriche e quelle iperboliche (basate sul numero e), stabilisce che cos(x) + j sen(x) = e^jx dove x è un numero reale e j è l’unità immaginaria. Ponendo x = p si ottiene la celebre relazione -1 = e^jp che lega mirabilmente fra loro l’unità negativa, quella immaginaria ed i numeri trascendenti e e p.

[3]⁾ Due numeri complessi si dicono coniugati quando hanno la stessa parte reale e la parte immaginaria pure uguale ma con segno cambiato.