Capitolo 19 ) Risonanza e instabilità
Si è visto che i blocchi normalizzati quali la struttura biquadratica permettono la costruzione, mediante opportune trasformazioni algebriche, di qualsiasi funzione di trasferimento di cui sia nota la forma generalizzata.
Naturalmente il blocco stesso deve poter svolgere le operazioni fondamentali richieste dalle relazioni differenziali insite nelle funzioni di trasferimento, in particolare l’integrazione e la derivazione.
Anche se già accennato precedentemente, è opportuno insistere su questi aspetti per meglio comprendere le caratteristiche del blocco e l’influenza dei vari coefficienti.
Riferendoci dunque ad una struttura biquadratica (pag. 18-1)

è immediato riconoscere che ponendo a 0 i coefficienti a2 e b2 la struttura si riduce ad una del primo ordine

con cui si possono svolgere:
- l’integrazione pura ad approssimazione rettangolare, ponendo a1=0 e b1=1
Infatti ![]() si trasforma
nel tempo in yt = yt-1 + a0·xt
si trasforma
nel tempo in yt = yt-1 + a0·xt
in cui intuitivamente yt-1 (l’uscita all’istante che precede t) è la ‘memoria’, cioè
la sommatoria di tutte le uscite precedenti, cui si aggiunge il valore d’ingresso
all’istante t moltiplicato per a0 , che rappresenta la costante d’integrazione.[1])
- l’integrazione pura ad approssimazione trapezoidale, ponendo a0=1/2 , a1=1/2
e b1=1.
Infatti
 si trasforma nel
tempo in yt = yt-1
+ (xt+xt-1)/2
si trasforma nel
tempo in yt = yt-1
+ (xt+xt-1)/2
che rappresenta una maggior approssimazione rispetto all’algoritmo precedente
(per semplicità si assume che la costante d’integrazione sia unitaria).
- la derivazione pura, ponendo a0 = 1/DT , a1 = - 1/DT e b1 = 0.
Infatti
![]() si trasforma
nel tempo in yt = (xt - xt-1)/ DT
si trasforma
nel tempo in yt = (xt - xt-1)/ DT
che non è altro che la derivazione alle differenze finite.
- la costante di tempo, ponendo a0 = DT/(T+DT), a1 =0 e b1 = T/(T+DT)
Infatti
 si trasforma
nel tempo in
si trasforma
nel tempo in
yt = yt-1·T/(T+DT) + xt·DT/(T+DT)
che è lo stesso algoritmo visto a pag. 17-3.
Possiamo vedere b1 (che risulta sempre <1) come il decadimento della memoria
yt-1 , mentre a0 rappresenta l’accrescimento dovuto al segnale d’ingresso xt,
entrambi durante l’intervallo DT. Nel caso di ingresso a gradino il risultato è un andamento esponenziale che tende al valore d’ingresso.
Si noti infatti che a0 + b1 = 1, il che fa tendere all’equilibrio quando il decadimento dell’uscita praticamente uguaglia l’incremento dell’ingresso.
Una maggior approssimazione è ottenibile ponendo a0 = 1 - e -DT/T e b1 = e -DT/T
valori che tengono conto dell’andamento esponenziale anche all’interno dell’intervallo DT.
Tornando alla struttura biquadratica completa, si può osservare che questa si rende necessaria per tener conto di casi in cui le soluzioni non sono reali ma complesse coniugate.
Se si considera il caso di due costanti di tempo reali, si può indifferentamente utilizzare il prodotto di due strutture del primo ordine oppure una struttura biquadratica completa, ma quest’ultima è la sola possibile ove le costanti non siano reali.
Esaminiamo prima il caso di due costanti di tempo reali T1 e T2.
La Fig 19.1 mostra la conversione algebrica della relativa funzione di trasferimento H(s) nei coefficienti del denominatore di una H(z) biquadratica.
Per inciso si segnala che tali trasformazioni sono eseguibili direttamente in Mathcadâ, utilizzando le possibilità offerta da questo nell’elaborazione simbolica delle espressioni algebriche, quali la sostituzione di variabile (Substitute for Variable), l’espansione in somma di termini (Expand Expression) e la successiva raccolta in potenze (Collect on Subexpression).
I risultati sono le espressioni di b1 e b2 in funione delle costanti T1, T2 e DT.
Analogamente è possibile ricavare viceversa le espressioni di T1 e T2 in funzione di b1 , b2 e DT.
Da queste ultime si può notare che, con b1 e b2 reali, la radice quadrata impone
il vincolo b12 + 4·b2 ³ 0 per ottenere soluzioni reali di T.
|
|
Fig. 19.1 - Espressioni per il calcolo dei coefficienti biquadratici date le costanti di tempo e viceversa.
Se tale vincolo non è rispettato si ottengono evidentemente valori di T1 e T2 con una parte immaginaria di segno opposto, cioè due valori complessi coniugati.
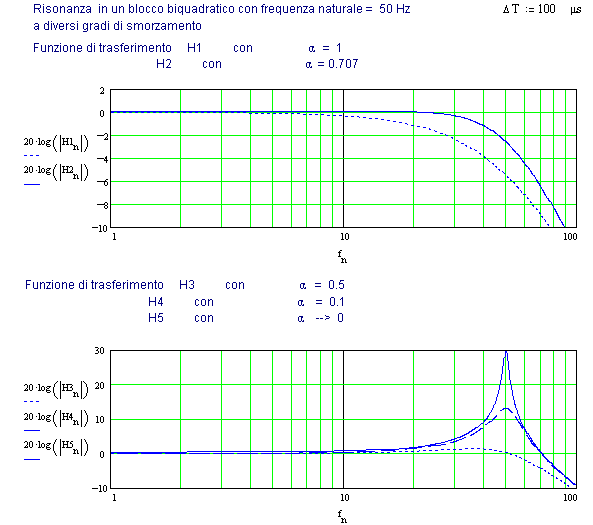
L’effetto di questo sull’andamento della funzione di trasferimento H(z) è un aumento del valore del modulo che può assumere l’aspetto di un picco all’intorno di una frequenza che viene chiamata frequenza di risonanza.
La risposta nel tempo ad un impulso o ad un gradino diventa in questo caso oscillante, indicando che il blocco è caratterizzato da elementi che si scambiano vicendevolmente energia .
Il più semplice esempio meccanico è una massa appesa ad una molla: se il sistema viene perturbato applicando alla molla una forza che varia la posizione della massa, quando si toglie tale forza il sistema torna alla posizione iniziale ma con movimenti oscillanti attorno a questa.
Tali oscillazioni sono ‘smorzate’, cioè la loro ampiezza si riduce man mano fino praticamente ad annullarsi, solo se esiste un elemento dissipatore dell’energia che alternativamente viene scambiata fra la molla (energia elastica) e la massa in movimento (energia inerziale), altrimenti le oscillazioni permarrebbero indefinitamente.
|
|
Fig. 19.2 - Risonanza in un blocco biquadratico.
Un esempio analogo nei circuiti elettrici è rappresentato dallo scambio di energia fra induttanze e capacità: solo la presenza di resistenze dissipatrici porta alla riduzione delle oscillazioni.
Si comprende quindi che in presenza di fenomeni oscillatori il concetto di costanti di tempo perda di significato e che per il loro studio sia più utile introdurre altri parametri quali la frequenza naturale (fnat) e il fattore di smorzamento (a, damping factor).
La Fig. 19.2 riporta le espressioni di calcolo dei coefficienti del blocco biquadratico (ridotto a 3 coefficienti, cioè considerando solo la parte passa-basso), in funzione di tali parametri.
Le espressioni sono state ricavate considerando al posto delle costanti di tempo T1 e T2 le equivalenze
![]()
![]()
Si noti che pur essendo T1 e T2 numeri complessi, i due parametri risultano reali. Infatti la radice quadrata del prodotto di due numeri complessi coniugati equivale al modulo e la loro somma equivale al doppio della parte reale.
La frequenza naturale (in Hz) corrisponde dunque alla frequenza di oscillazione permanente che il sistema avrebbe in mancanza di smorzamento, mentre il coefficiente di smorzamento è dato dal rapporto fra la parte reale delle costanti di tempo (ovviamente uguale per entrambe) ed il loro modulo (radice quadrata della somma dei quadrati della parte reale e della parte immaginaria).
Quest’ultimo può perciò variare da 0 a 1: precisamente a= 0 quando la parte reale è zero (caso di smorzamento nullo, quindi con oscillazioni permanenti) e a=1 quando la parte immaginaria è zero (cioè T1 e T2 coincidenti e reali).
Se la parte reale è negativa, e quindi è negativo a, si ha instabilità, cioè il blocco, una volta eccitato, oscilla con ampiezze crescenti e non torna più in equilibrio.
Questa possibilità, dovuta alla reazione propria del blocco ricorsivo, deve essere attentamente evitata e nella determinazione dei coefficienti di ciascun blocco deve essere verificato che ciò non accada in nessun caso.
La Fig. 19.2 mostra anche il calcolo della frequenza di risonanza, cioè di quel valore di frequenza per cui il modulo della funzione di trasferimento diventa massimo, cioè del picco nel diagramma di Bode.
Tale valore varia in funzione di a e coincide con la frequenza naturale solo per a=0, diminuendo poi fino alla frequenza zero.
Si osservi che questa si ha per a=1/Ö2@0.707 in quanto la radice nella formula della frequenza di risonanza impone questo massimo. Tale valore corrisponde allo smorzamento critico, non più oscillante ma che presenta nel caso di ingresso a gradino una sovraelongazione dell’uscita prima di stabilizzarsi al valore finale.
Per tutti i valori compresi fra
questo ed 1, la sovraelongazione si riduce fino ad annullarsi (a=1).
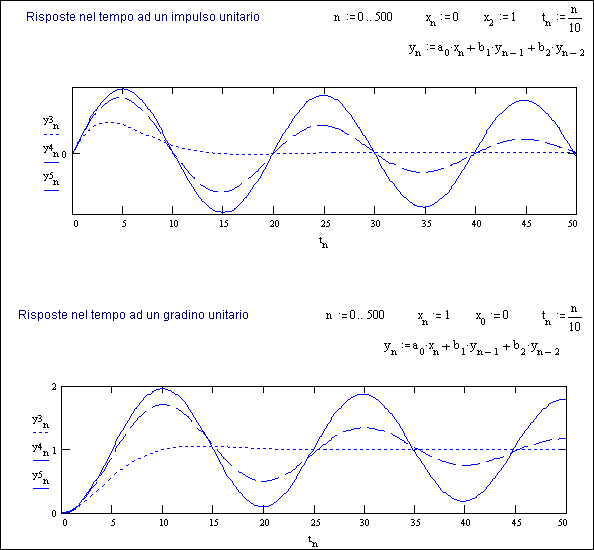
Per una migliore comprensione dei vari casi citati la Fig. 19.3 riporta per ciascuno sia il diagramma di Bode del modulo (Fig.19.3a), sia le risposte nel tempo all’impulso e al gradino (Fig.19.3b, solo nei casi di risonanza).
Non viene illustrato il caso di instabilità perchè ritenuto intuitivo.
I casi di smorzamento nullo (H1) e di smorzamento critico (H2) sono illustrati nel primo diagramma (con scala delle ampiezze in dB amplificata) per evidenziare l’allargamento della banda passante. La conseguenza è una maggiore rapidità di risposta di H2 rispetto ad H1.
|
|
Fig. 19.3a - Diagrammi di blocchi biquadratici risonanti.
Nel secondo diagramma sono rappresentati 3 casi di risonanza H3, H4 ed H5, a diverso grado di smorzamento.
Il valore massimo del picco è molto influenzato sia dal tempo di scansione (è stato qui utilizzato DT=100 ms) che dalla precisione dei coefficienti, quindi da qualsiasi troncamento dei dati calcolati.
La frequenza naturale è stata nell’esempio stabilita a 50 Hz ed è infatti vicino a questo valore che si trovano i picchi di risonanza (se a tende a zero la frequenza di risonanza tende a quella naturale).
La Fig. 19.3b mostra i segnali d’uscita y3, y4 ed y5 ottenuti applicando rispettivamente ad H3, H4 ed H5 dapprima un segnale d’ingresso x ad impulso unitario (primo grafico) e poi un segnale x a gradino unitario (secondo grafico).
In entrambi i casi è stata utilizzata per ricavare y la medesima equazione ricorsiva, funzione com’è noto dei coefficienti a0, b1 e b2 della particolare H(z), nonchè dei valori di y negli istanti precedenti.
|
|
Fig. 19.3b - Risposte nel tempo di blocchi biquadratici risonanti.
L’unica variante nei due grafici è la definizione di x , che per il primo è sempre zero fuorchè all’istante n=2 in cui viene posto uguale ad 1, quindi un impulso che dura un intervallo di scansione, mentre nel secondo è sempre 1 fuorchè all’istante iniziale, quindi un gradino.
Naturalmente i calcoli degli y (non mostrati nella figura) devono iniziare dall’istante n=2, per non avere indici negativi.
Per poter svolgere i calcoli i valori iniziali di y0 e y1 devono essere posti a zero.
La scala dei tempi è determinata da n·DT, e poichè l’intervallo di scansione è stato fissato in 100 ms, l’unità di tn risulta in ms.
Si può infatti notare che il
periodo di oscillazione è all’incirca
di 20 ms.[2])
L’esame dell’influenza dei vari coefficienti del blocco biquadratico ha finora riguardato il denominatore, cioè i coefficienti b, che caratterizzano, come visto, un generico comportamento passa-basso o di tipo integrale.
L’unico coefficiente considerato non zero del numeratore, a0, è stato utilizzato per fissare il ‘guadagno’ di tutto il blocco, cioè per fissare nel diagramma di Bode la posizione di tutto il grafico rispetto la retta di 0 dB.
Si è però già accennato al fatto che il numeratore rappresenta la parte derivativa o passa-alto. Se infatti si pone semplicemente a1 = -a0 si aggiunge all’azione del denominatore un effetto derivatore puro, che azzera il guadagno a frequenza zero.
Come visto alla Fig. 18.4 , questo porta ad un filtro passa-banda
|
|
Fig. 19.4 - Semplice filtro passa-banda con l’utilizzo di un blocco biquadratico.
Se a questo si aggiunge l’effetto di risonanza, si possono ottenere filtri altamente selettivi.
Per trattare questi ultimi è però prima opportuno definire un’ulteriore forma di parametrizzazione dei coefficienti del blocco biquadratico.
Se si considera la funzione di trasferimento H(z) come un’equazione, se ne possono ricavare gli zeri (soluzioni di z ottenute ponendo uguale a zero il numeratore) ed i poli (soluzioni di z ottenute ponendo uguale a zero il denominatore, quindi rendendo infinita la funzione).
Questi valori, rappresentabili nel piano complesso z, hanno precisi significati nel comportamento del blocco.
La Fig. 19.5 mostra tali rappresentazioni in forma di vettori polari, definiti cioè ciascuno dal modulo r e dall’angolo Q. Poichè, data la struttura biquadratica, tali valori possono essere o reali o coppie complesse coniugate, o risultano direttamente sull’asse orizzontale o sono simmetrici rispetto a questo.
Il cerchio rappresenta il luogo dei punti per cui r=1, mentre l’angolo Q rappresenta l’incremento angolare di ciascuna freqenza durante l’intervallo di campionamento, Q = 2·p·f ·DT.

Fig. 19.5 - Rappresentazione di zeri e poli di un
blocco biquadratico
nel piano z.
Nei casi di soluzioni complesse coniugate le relazioni fra poli e zeri rispetto ai coefficienti a e b sono:
zeri 

poli ![]()

e rispettivamente, dati r e Q
a0 =
1 a1 = -2·rz·cos(Qz) a2 = rz2
b1
= 2·rp·cos(Qp) b2
= rp2
Con i dati della Fig. 19.4, b1=1.7 e b2= - 0.75 , si avrebbe rp=0.866 e Qp = 0.183 (@11°), mentre per il numeratore, essendo di primo ordine e con soluzione reale, si ricaverebbe direttamente rz=1 e Qz = 0.
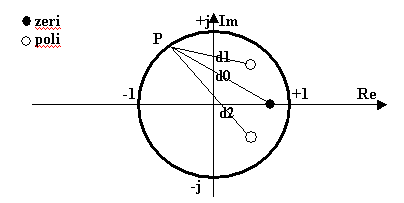
Fig. 19.6 - Interpretazione geometrica di z e di H(z) nel
piano complesso.
L’interpretazione geometrica che si può dare alla rappresentazione nel piano complesso ( Fig. 19.6) è che un generico punto P sul cerchio unitario corrisponde alla z di una data frequenza (z=ej·2p·f·DT) e, nel caso in cui vi sia un solo zero, che il modulo della funzione H(z) corrisponde al rapporto della distanza fra il punto e lo zero (d0) ed il prodotto delle distanze fra il punto ed i poli ( d1·d2).
Ciò può essere ricavato scrivendo la funzione H(z) con lo zero e i poli in forma polare:
1 - rz · z-1
![]() H(z) =
H(z) =
(1 - rp · ej·Qp· z-1) · (1 - rp · e-j·Qp· z-1)
Sostituendo poi z-1 = e-j·Q (dove Q=2·p·f·DT ed il corrispondente r=1) si ottiene
1 - rz · e-j·Q
![]() H(z) =
H(z) =
(1 - rp · ej·Qp· e-j·Q) · (1 - rp · e-j·Qp· e-j·Q)
cioè
½( ej·Q - rz) · ej·Q ½
![]() ½H(z)½
=
½H(z)½
=
½(ej·Q - rp · ej·Qp) · (ej·Q - rp · e-j·Qp)
½
da cui risulta che i moduli del numeratore e del denominatore corrispondono alle distanze sopra definite (ej·Q è il vettore di P, rp · ej·Qp il vettore del primo polo, ecc.).
Questa parametrizzazione in funzione dei poli e dello zero, consente importanti considerazioni.
La prima è che la risonanza è tanto più elevata quanto rp tende ad 1.
Con rp=1 si ha un’oscillazione permanente e per rp>1 si ha instabilità.
Un’altra è che se rz=1 si ha H(z)=0 a frequenza zero, cioè si ha il caso già visto di blocco della componente continua.
La più importante è però quella che riguarda il caso di guadagno costante in corrispondenza della risonanza, indipendentemente dalla frequenza di risonanza.
Se infatti si pone Qr=2·p·fr·DT, rz=cos(Qr) e Qp=Qr, si ottiene che il modulo di H(z) rimane praticamente invariato a qualsiasi fr.
Ciò è dimostrabile geometricamente nel campo z osservando che in questo caso, purchè vi sia netta risonanza cioè che rp tenda ad 1, la distanza d2 è praticamente il doppio di d0, e che d1 si riduce a 1-rp.
In sostanza si ha in questo caso in corrispondenza di fr
1
![]() ½H(z)½ @
½H(z)½ @
2·(1-rp)
|
|
Fig. 19.7 - Risonatore a guadagno indipendente dalla frequenza di risonanza.
Ciò ha una notevole importanza pratica perchè permette di progettare filtri altamente selettivi con banda e guadagno ben definiti.
La Fig. 19.7 è un esempio di tali filtri, in cui si è stabilita una frequenza naturale (qui uguale a quella di risonanza) di 50 Hz e si è imposto un guadagno 1 in corrispondenza di questa.
La scelta di r=0.98 (quindi molto vicino ad 1) condiziona sia il guadagno che la banda passante.
Il risultato è visibile nel diagramma di Bode oppure, per confronto, in diagramma lineare. La selettività ottenuta è evidente.