Capitolo 5 ) Spettri di impulsi rettangolari

Fra le forme d’onda trasformabili in spettri di frequenza rivestono particolare importanza gli impulsi rettangolari.

Questi permettono anche di comprendere meglio il significato fisico del contenuto armonico.

Se infatti è ovvio che un segnale perfettamente sinusoidale ha come spettro un solo segmento (l’ampiezza del segnale stesso in corrispondenza della fondamentale), è intuibile che un segnale perfettamente rettangolare abbia una serie infinita di armoniche.

La suddivisione del periodo in N intervalli di campionamento influisce però sulla forma dell’impulso e ne limita anche il contenuto armonico.

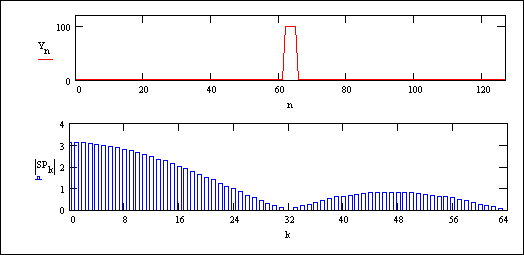
Nell’esempio della Fig. 5.1 , in cui N=128 , l’impulso ha una forma trapezia, con tempi di salita e di discesa di 1/128 del periodo.

Dall’analisi di Fourier si è visto (pag. 10) che il numero K di armoniche ricavabili è uguale a N/2 - 1 , quindi in questo caso oltre alla componente continua si possono calcolare al massimo 63 armoniche.

Aumentando N si ha una sempre maggiore approssimazione all’impulso rettangolare, con un conseguente incremento del numero di armoniche.

L’ampiezza, o modulo, di ciascuna armonica è rappresentabile nello spettro di frequenza, riportato nel secondo grafico della stessa Fig. 5.1.

E’ interessante notare come varia la forma di questo spettro al variare della durata dell’impulso rispetto al periodo.

La Fig. 5.2 rappresenta il caso di un impulso di durata doppia e la Fig. 5.3 di durata quadrupla di quello della Fig. 5.1.

Si nota che lo spettro tende a concentrarsi verso lo zero, aumentando i moduli delle frequenze più basse e diminuendo quelli delle frequenze più alte (attenzione alla variazione delle scale verticali).

Per approfondire questo argomento si può utilizzare un impulso di area unitaria cioè di durata T e di ampiezza 1/T .

Supponendo inoltre che il periodo sia infinito (considerando così un solo impulso anzichè una serie di impulsi), si può applicare il metodo d’integrazione di pag. 19, osservando che il segnale y(t) in questo caso ha ampiezza zero fra - ¥ e - T/2, ampiezza 1/T fra - T/2 e + T/2, e ancora ampiezza zero fra +T/2 e + ¥.

Si ha perciò:

Fig. 5.1 - Spettro di frequenza (solo modulo) di un impulso di durata 2·DT.

Fig. 5.2 - Spettro di frequenza nel caso di impulso di durata 4·DT.

Fig. 5.3 - Spettro di frequenza nel caso di impulso di durata 8·DT.

Ricorrendo alla formula di Eulero ( nota 1 del capitolo 2 ), il risultato può essere espresso in forma trigonometrica anzichè esponenziale:

sen (w·T/2)

G(jw) =

w·T/2

La Fig. 5.4 rappresenta appunto la variazione degli spettri continui G(jw) al variare della durata T dell’impulso di area unitaria.

Gli spettri sono stati limitati nei grafici fra -1.6 Hz a +1.6 Hz , ma la loro estensione va da - ¥ a + ¥.

Estrapolando i risultati della Fig. 5.4 si possono ricavare due importanti osservazioni.

Se la durata dell’impulso tende all’infinito (e quindi la sua ampiezza tende a zero) si ha uno spettro costituito da un solo segmento, di ampiezza 1, in corrispondenza della frequenza ‘zero’.

Infatti il segnale è in questo caso ‘continuo’, senza alcuna armonica.

Se viceversa la durata dell’impulso tende a zero (e la sua ampiezza all’infinito), si ha uno spettro uniforme, di ampiezza 1, per qualsiasi armonica da - ¥ a + ¥.

Quest’ultimo caso rappresenta la funzione d o di Dirac ( perchè utilizzata da Dirac nella meccanica quantistica), la cui definizione matematica è

e con lo spettro G(jw) = 1

Fig. 5.4 - Esempi di spettri continui di impulsi unitari di varia durata.